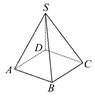
分两步,先将四棱锥一侧面三顶点染色,然后再分类考虑另外两顶点的染色数,用乘法原理可求解.
由题设,四棱锥S-ABCD的顶点S,A,B所染的颜色互不相同,它们共有5×4×3=60种染色方法.
当S,A,B染好时,不妨设所染颜色依次为1,2,3,若C染2,则D可染3或4或5,有3种染法;若C染4,则D可染3或5,有2种染法;若C染5,则D可染3或4,有2种染法,即当S,A,B染好时,C,D还有7种染法.
故不同的染色方法有60×7=420种.
【一题多解】以S,A,B,C,D的顺序分步染色.
第一步,S点染色,有5种方法;
第二步,A点染色,与S在同一条棱上,有4种方法;
第三步,B点染色,与S,A分别在同一条棱上有3种方法;
第四步,C点染色,也有3种方法,但考虑到D点与S,A,C相邻,需针对A与C是否同色进行分类,当A与C同色时,D点有3种染色方法,当A与C不同色时,因为C与S,B也不同色,所以C点有2种染色方法,D点也有2种染色方法.
由分步乘法计数原理,分类加法计数原理,得共有5×4×3×(1×3+2×2)=420种不同方法.
【方法技巧】涂色问题的两种解题方案
一是选择正确的涂色顺序,按步逐一涂色,这时用分步乘法计数原理逐一计数.
二是根据涂色时用颜色的多少,进行分类处理,这时用分类加法计数原理进行计数.
注意点:在分步涂色时,要尽量让相邻区域多的区域先涂,在分类涂色时要注意不相邻区域的颜色可相同也可不同,这是所用颜色多少的依据.



 备战中考寒假系列答案
备战中考寒假系列答案