
【题目】已知等差数列{an}的前n项和为Sn,等比数列{bn}的前n项和为Tn,a1=﹣1,b1=1,a2+b2=2.
(1)若a3+b3=5,求{bn}的通项公式;
(2)若T3=21,求S3.
【答案】(1)![]() ;(2)21
;(2)21
【解析】试题分析: ![]() 设等差数列
设等差数列![]() 的公差为
的公差为![]() ,等比数列
,等比数列![]() 的公比为
的公比为![]() ,运用等差数列和等比数列的通项公式,列方程解方程可得
,运用等差数列和等比数列的通项公式,列方程解方程可得![]() ,即可得到所求通项公式;
,即可得到所求通项公式;
![]() 运用等比数列的求和公式,解方程可得公比,再由等差数列的通项公式和求和,计算即可得答案。
运用等比数列的求和公式,解方程可得公比,再由等差数列的通项公式和求和,计算即可得答案。
解析:(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,
a1=﹣1,b1=1,a2+b2=2,a3+b3=5,可得﹣1+d+q=2,﹣1+2d+q2=5,
解得d=1,q=2或d=3,q=0(舍去),
则{bn}的通项公式为bn=2n﹣1,n∈N*;
(2)b1=1,T3=21,可得1+q+q2=21,解得q=4或﹣5,
当q=4时,b2=4,a2=2﹣4=﹣2,
d=﹣2﹣(﹣1)=﹣1,S3=﹣1﹣2﹣3=﹣6;
当q=﹣5时,b2=﹣5,a2=2﹣(﹣5)=7,
d=7﹣(﹣1)=8,S3=﹣1+7+15=21.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
【题目】某课外实习作业小组调查了1000名职场人士,就入职两家公司的意愿做了统计,得到如下数据分布:
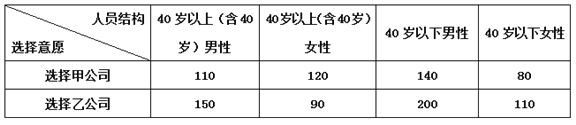
(1)请分别计算40岁以上(含40岁)与40岁以下全体中选择甲公司的频率(保留两位小数),根据计算结果,你能初步得出什么结论?
(2)若分析选择意愿与年龄这两个分类变量,计算得到的![]() 的观测值为
的观测值为![]() ,测得出“选择意愿与年龄有关系”的结论犯错误的概率的上限是多少?并用统计学知识分析,选择意愿与年龄变量和性别变量哪一个关联性更大?
,测得出“选择意愿与年龄有关系”的结论犯错误的概率的上限是多少?并用统计学知识分析,选择意愿与年龄变量和性别变量哪一个关联性更大?
附: 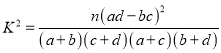

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1: ![]() (t为参数,t≠0),其中0≤α<π.在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sin θ,C3:ρ=2
(t为参数,t≠0),其中0≤α<π.在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sin θ,C3:ρ=2![]() cos θ.
cos θ.
(1)求C2与C3交点的直角坐标;
(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆与抛物线y2=![]() x有一个相同的焦点,且该椭圆的离心率为
x有一个相同的焦点,且该椭圆的离心率为![]() .
.
(1)求椭圆的标准方程;
(2)过点P(0,1)的直线与该椭圆交于A,B两点,O为坐标原点,若![]() ,求△AOB的面积.
,求△AOB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理, ![]() 得到下表2:
得到下表2:
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求z关于t的线性回归方程;
(Ⅱ)通过(Ⅰ)中的方程,求出y关于x的回归方程;
(Ⅲ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中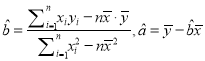 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为坐标原点,动点
为坐标原点,动点![]() 在椭圆
在椭圆![]() 上,过
上,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 满足
满足![]() .(Ⅰ)求点
.(Ⅰ)求点![]() 的轨迹方程
的轨迹方程![]() ;
;
(Ⅱ)过![]() 的直线
的直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 两点,过
两点,过![]() 作与
作与![]() 垂直的直线
垂直的直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 两点,求证:
两点,求证: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com