
【题目】已知函数![]()
![]() 讨论函数
讨论函数![]() 的单调性;
的单调性;
![]() 设
设![]() ,对任意
,对任意![]() 的恒成立,求整数
的恒成立,求整数![]() 的最大值;
的最大值;
![]() 求证:当
求证:当![]() 时,
时,![]()
【答案】(1)当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(2)
上单调递减;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(2)若a≤0,则f(1)=﹣a+1>0,不满足f(x)≤0恒成立.若a>0,由(Ⅰ)可知,函数f(x)在(0,![]() )上单调递增;在(
)上单调递增;在(![]() )上单调递减.由此求出函数的最大值,由最大值小于等于0可得实数a的取值范围.
)上单调递减.由此求出函数的最大值,由最大值小于等于0可得实数a的取值范围.
(3)由(2)可知,当a=1时,f(x)≤0恒成立,即lnx﹣x+1≤0.得到﹣xlnx≥﹣x2+x,则ex﹣xlnx+x﹣1≥ex﹣x2+2x﹣1.然后利用导数证明ex﹣x2+2x﹣1>0(x>0),即可说明ex﹣xlnx+x>0.
(1)∵函数 f(x)=![]() (a∈R ).
(a∈R ).
∴![]() ,x>0,
,x>0,
当a=0时,f′(x)![]() 0,f(x)在(0,+∞)单调递增.
0,f(x)在(0,+∞)单调递增.
当a>0时,f′(x)>0,f(x)在(0,+∞)单调递增.
当a<0时,令f′(x)>0,解得:0<x![]() ,
,
令f′(x)<0,解得:x![]() ,
,
故f(x)在(0,![]() )递增,在(
)递增,在(![]() ,+∞)递减.
,+∞)递减.
(2)当![]() 时,则f(1)=2a+3>0,不满足f(x)≤0恒成立.
时,则f(1)=2a+3>0,不满足f(x)≤0恒成立.
若a<0,由(1)可知,函数f(x)在(0,![]() )递增,在(
)递增,在(![]() ,+∞)递减.
,+∞)递减.
∴![]() ,又f(x)≤0恒成立,
,又f(x)≤0恒成立,
∴f(x)max≤0,即![]() 0,令g(a)=
0,令g(a)=![]() ,则g(a)单调递增,g(-1)=1,
,则g(a)单调递增,g(-1)=1,
g(-2)=![]() <0,∴a
<0,∴a![]() 时,g(a) <0恒成立,此时f(x)≤0恒成立,
时,g(a) <0恒成立,此时f(x)≤0恒成立,
∴整数![]() 的最大值-2.
的最大值-2.
(3)由(2)可知,当a=-2时,f(x)≤0恒成立,即lnx﹣2x2+1≤0.即xlnx﹣2x3+x≤0,![]() 恒成立,①
恒成立,①
又![]() ex﹣x2+2x﹣1+(
ex﹣x2+2x﹣1+(![]() )
)
∴只需证ex﹣x2+2x﹣1![]() ,
,
记g(x)=ex﹣x2+2x﹣1(x>0),则g′(x)=ex﹣2x+2,
记h(x)=ex﹣2x+2,则h′(x)=ex﹣2,由h′(x)=0,得x=ln2.
当x∈(0,ln2)时,h′(x)<0;当x∈(ln2,+∞)时,h′(x)>0.
∴函数h(x)在(0,ln2)上单调递减;在(ln2,+∞)上单调递增.
∴![]() 4﹣2ln2>0.
4﹣2ln2>0.
∴h(x)>0,即g′(x)>0,故函数g(x)在(0,+∞)上单调递增.
∴g(x)>g(0)=e0﹣1=0,即ex﹣x2+2x﹣1>0.
结合①∴ex﹣x2+2x﹣1+(![]() )>0,即
)>0,即![]() >0成立.
>0成立.


 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l1:kx-y+4=0与直线l2:x+ky-3=0相交于点P,则当实数k变化时,点P到直线4x-3y+10=0的距离的最大值为( )
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在教材中,我们已研究出如下结论:平面内![]() 条直线最多可将平面分成
条直线最多可将平面分成![]() 个部分.现探究:空间内
个部分.现探究:空间内![]() 个平面最多可将空间分成多少个部分,
个平面最多可将空间分成多少个部分,![]() .设空间内
.设空间内![]() 个平面最多可将空间分成
个平面最多可将空间分成![]() 个部分.
个部分.
(1)求![]() 的值;
的值;
(2)用数学归纳法证明此结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以椭圆![]() :
:![]() 的中心
的中心![]() 为圆心,
为圆心,![]() 为半径的圆称为该椭圆的“准圆”.设椭圆
为半径的圆称为该椭圆的“准圆”.设椭圆![]() 的左顶点为
的左顶点为![]() ,左焦点为
,左焦点为![]() ,上顶点为
,上顶点为![]() ,且满足
,且满足![]() ,
,![]() .
.
(1)求椭圆![]() 及其“准圆”的方程;
及其“准圆”的方程;
(2)若椭圆![]() 的“准圆”的一条弦
的“准圆”的一条弦![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,试证明:当
两点,试证明:当![]() 时,弦
时,弦![]() 的长为定值.
的长为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代有着辉煌的数学研究成果,其中的《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、《缉古算经》,有丰富多彩的内容,是了解我国古代数学的重要文献,这5部专著中有3部产生于汉、魏、晋、南北朝时期,某中学拟从这5部专著中选择2部作为“数学文化”校本课程学习内容,则所选2部专著中至少有一部是汉、魏、晋、南北朝时期专著的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex![]() (x﹣a)2+4.
(x﹣a)2+4.
(1)若f(x)在(﹣∞,+∞)上单调递增,求a的取值范围;
(2)若x≥0,不等式f(x)≥0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面是正方形,侧棱
的底面是正方形,侧棱![]() 底面
底面![]() ,过
,过![]() 作
作![]() 垂直
垂直![]() 交
交![]() 于
于![]() 点,作
点,作![]() 垂直
垂直![]() 交
交![]() 于
于![]() 点,平面
点,平面![]() 交
交![]() 于
于![]() 点,点
点,点![]() 为
为![]() 上一动点,且
上一动点,且![]() ,
,![]() .
.
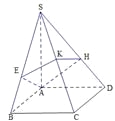
(1)试证明不论点![]() 在何位置,都有
在何位置,都有![]() ;
;
(2)求![]() 的最小值;
的最小值;
(3)设平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com