
【题目】某公司为对本公司的160名员工的身体状况进行调查,先将员工随机编号为1,2,3,…,159,160,采用系统抽样的方法(等间距地抽取,每段抽取一个个体)将抽取的一个样本.已知抽取的员工中最小的两个编号为5,21,那么抽取的员工中,最大的编号应该是( )
A.141
B.142
C.149
D.150
科目:高中数学 来源: 题型:
【题目】①设三个正实数a , b , c , 满足![]() ,求证:a , b , c一定是某一个三角形的三条边的长;
,求证:a , b , c一定是某一个三角形的三条边的长;
②设n个正实数 a1,a2,...an 满足不等式 ![]() (其中
(其中 ![]() ),求证: a1,a2,...an 中任何三个数都是某一个三角形的三条边的长.
),求证: a1,a2,...an 中任何三个数都是某一个三角形的三条边的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线mx+ ![]() y﹣1=0在y轴上的截距是﹣1,且它的倾斜角是直线
y﹣1=0在y轴上的截距是﹣1,且它的倾斜角是直线 ![]() =0的倾斜角的2倍,则( )
=0的倾斜角的2倍,则( )
A.m=﹣ ![]() ,n=﹣2
,n=﹣2
B.m= ![]() ,n=2
,n=2
C.m= ![]() ,n=﹣2
,n=﹣2
D.m=﹣ ![]() ,n=2
,n=2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是各项为正数的等比数列,{bn}是等差数列,且a1=b1=1,b2+b3=2a3 , a5﹣3b2=7.
(1)求{an}和{bn}的通项公式;
(2)设cn=anbn , n∈N* , 求数列{cn}的前n项和为Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是 ![]() ,D是AC的中点.
,D是AC的中点.
(1)求证:B1C∥平面A1BD;
(2)求二面角A1﹣BD﹣A的大小;
(3)求直线AB1与平面A1BD所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x﹣4y+3=0.
(1)若圆C的切线在x轴、y轴上的截距相等,求切线的方程;
(2)从圆C外一点P(x1 , y1)向圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使|PM|最小的点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F2、F1是双曲线 ![]() =1(a>0,b>0)的上、下焦点,点F2关于渐近线的对称点恰好落在以F1为圆心,|OF1|为半径的圆上,则双曲线的离心率为( )
=1(a>0,b>0)的上、下焦点,点F2关于渐近线的对称点恰好落在以F1为圆心,|OF1|为半径的圆上,则双曲线的离心率为( )
A.3
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限x年 | 3 | 5 | 6 | 7 | 9 |
年推销金额y万元 | 2 | 3 | 3 | 4 | 5 |
(1)从编号1﹣5的五位推销员中随机取出两位,求他们年推销金额之和不少于7万元的概率;
(2)求年推销金额y关于工作年限x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;若第6名产品推销员的工作年限为11年,试估计他的年推销金额. 附:回归直线的斜率和截距的最小二乘法估计公式为:
;若第6名产品推销员的工作年限为11年,试估计他的年推销金额. 附:回归直线的斜率和截距的最小二乘法估计公式为: ![]() =
= 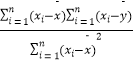 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:在数列{an}中,若an2﹣an﹣12=p,(n≥2,n∈N* , p为常数),则称{an}为“等方差数列”,下列是对“等方差数列”的有关判断:
①若{an}是“等方差数列”,则数列{ ![]() }是等差数列;
}是等差数列;
②{(﹣2)n}是“等方差数列”;
③若{an}是“等方差数列”,则数列{akn}(k∈N* , k为常数)也是“等方差数列”;
④若{an}既是“等方差数列”,又是等差数列,则该数列是常数数列.
其中正确命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com