
|
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
|
A、(0,±
| ||
B、(±
| ||
C、(0,±
| ||
D、(±
|
查看答案和解析>>
科目:高中数学 来源: 题型:
A、(0,
| ||||
B、(
| ||||
C、(0,
| ||||
D、[
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
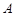 ,如果定义了一种运算“
,如果定义了一种运算“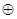 ”,使得集合
”,使得集合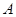 中的元素间满足下列4个条件:
中的元素间满足下列4个条件: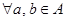 ,都有
,都有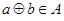 ;
; ,使得对
,使得对 ,都有
,都有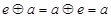 ;
; ,
, ,使得
,使得 ;
;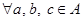 ,都有
,都有 ,
,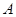 对于运算“
对于运算“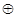 ”构成“对称集”.
”构成“对称集”.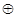 ”:
”: ,运算“
,运算“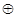 ”为普通加法;
”为普通加法; ,运算“
,运算“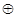 ”为普通减法;
”为普通减法; ,运算“
,运算“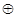 ”为普通乘法.
”为普通乘法.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com