练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】用5种不同的颜色给如图中所给出的四个区域涂色，每个区域涂一种颜色，若要求相邻（有公共边）的区域不同色，那么共有种不同的涂色方法．

    【答案】260
    【解析】解：对于1号区域，有5种颜色可选，即有5种涂法， 分类讨论其他3个区域：①若2、3号区域涂不同的颜色，则有A42=12种涂法，4号区域有3种涂法，此时其他3个区域有12×3=36种涂法；
    ②若2、3号区域涂相同的颜色，则有4种涂法，4号区域有4种涂法，此时其他3个区域有有4×4=16种涂法；
    则共有5×（36+16）=5×52=260种；
    故答案为：260．
    根据题意，先分析于1号区域，有5种颜色可选，即有5种涂法方案，再分①若2、3号区域涂不同的颜色，②若2、3号区域涂相同的颜色，两种情况讨论其他3个区域的涂色方案，由分类计数原理可得其他个区域的涂色方案的数目；再由分步计数原理计算可得答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，已知正方形ABCD的边长为6，点E，F分别在边AB，AD上，AE=AF=4，现将△AEF沿线段EF折起到△A′EF位置，使得A′C=2 ．

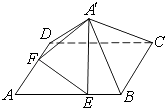
    （1）求五棱锥A′﹣BCDFE的体积；
    （2）求平面A′EF与平面A′BC的夹角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）

    某港湾的平面示意图如图所示， ， ， 分别是海岸线上的三个集镇， 位于的正南方向6km处， 位于的北偏东方向10km处．

    （Ⅰ）求集镇， 间的距离；

    （Ⅱ）随着经济的发展，为缓解集镇的交通压力，拟在海岸线上分别修建码头，开辟水上航线．勘测时发现：以为圆心，3km为半径的扇形区域为浅水区，不适宜船只航行．请确定码头的位置，使得之间的直线航线最短．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两人投篮命中的概率为别为 与 ，各自相互独立，现两人做投篮游戏，共比赛3局，每局每人各投一球．
    （1）求比赛结束后甲的进球数比乙的进球数多1个的概率；
    （2）设ξ表示比赛结束后，甲、乙两人进球数的差的绝对值，求ξ的概率分布和数学期望E（ξ）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列结论正确的是（ ）
    A.各个面都是三角形的几何体是三棱锥
    B.一平面截一棱锥得到一个棱锥和一个棱台
    C.棱锥的侧棱长与底面多边形的边长相等，则该棱锥可能是正六棱锥
    D.圆锥的顶点与底面圆周上的任意一点的连线都是母线

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，几何体中，为边长为的正方形，为直角梯形，，，，，．

    （1）求异面直线和所成角的大小；

    （2）求几何体的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点（1， ）是函数f（x）= ax（a＞0，a≠1）图象上一点，等比数列{an}的前n项和为c﹣f（n）．数列{bn}（bn＞0）的首项为2c，前n项和满足 = +1（n≥2）． （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）若数列{ }的前n项和为Tn ， 问使Tn＞ 的最小正整数n是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，设利用的旧墙的长度为x（单位：m），修建此矩形场地围墙的总费用为y（单位：元）． （Ⅰ）将y表示为x的函数：
    （Ⅱ）试确定x，使修建此矩形场地围墙的总费用最小，并求出最小总费用．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于函数f1（x），f2（x），h（x），如果存在实数a，b使得h（x）=af1（x）+bf2（x），那么称h（x）为f1（x），f2（x）的生成函数．
    （1）给出函数 ，h（x）是否为f1（x）， f2（x）的生成函数？并说明理由；
    （2）设 ，生成函数h（x）．若不等式3h2（x）+2h（x）+t＞0在x∈[2，4]上恒成立，求实数t的取值范围；
    （3）设 ，取a＞0，b＞0，生成函数h（x）图象的最低点坐标为（2，8）．若对于任意正实数x1 ， x2且x1+x2=1．试问是否存在最大的常数m，使h（x1）h（x2）≥m恒成立？如果存在，求出这个m的值；如果不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案