
分析 (1)先求出a=b,设出双曲线方程,根据$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=2$,求出a2=2,从而求出双曲线方程即可;(2)设出直线方程,联立方程组,结合韦达定理求出即可.
解答 解:(1)由e=$\sqrt{2}$⇒$\frac{c}{a}$=$\sqrt{2}$⇒c=$\sqrt{2}$a,b=$\sqrt{{c}^{2}{-a}^{2}}$=a,
故双曲线C的方程为x2-y2=a2(a>0).
由$\overrightarrow{P{F_2}}•\overrightarrow{{F_1}{F_2}}=0$⇒xp=c=$\sqrt{2}$a,yp=±a,又F1(-$\sqrt{2}$a,0),F2($\sqrt{2}$a,0),
$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=2$⇒a2=2,故得出双曲线C的方程为$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1.…(5分)
(2)由(1)知点F1、F2的坐标分别为(-2,0),(2,0),
当直线的斜率不存在时,得$\overrightarrow{{F}_{1}A}$•$\overrightarrow{{F}_{1}B}$=14;…(7分)
当直线的斜率存在时,设其方程为y=k(x-2),并设A(x1,k(x1-2)),B(x2,k(x2-2)),
由$\left\{\begin{array}{l}{y=k(x-2)}\\{{x}^{2}{-y}^{2}=2}\end{array}\right.$⇒(k2-1)x2-4k2x+4k2+2=0,依题意知k2-1≠0.
$\overrightarrow{{F}_{1}A}$•$\overrightarrow{{F}_{1}B}$=(x1+2,k(x1-2))(x2+2,k(x2-2))=(k2+1)x1x2-(2k2-2)(x1+x2)+4k2+4,
将x1+x2=$\frac{{4k}^{2}}{{k}^{2}-1}$,x1x2=$\frac{{4k}^{2}+2}{{k}^{2}-1}$代入上式化简得:
$\overrightarrow{{F}_{1}A}$•$\overrightarrow{{F}_{1}B}$=14+$\frac{12}{{k}^{2}-1}$,由k2≥0及k2≠1,$\overrightarrow{{F}_{1}A}$•$\overrightarrow{{F}_{1}B}$≤2或$\overrightarrow{{F}_{1}A}$•$\overrightarrow{{F}_{1}B}$>14,
综上可知$\overrightarrow{{F}_{1}A}$•$\overrightarrow{{F}_{1}B}$的取值范围是(-∞,2]∪[14,+∞).…(12分)
点评 本题考察了求双曲线的方程问题,考察直线和曲线的关系,是一道中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{34}{103}$ | B. | 100 | C. | $\frac{1}{100}$ | D. | $\frac{1}{104}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
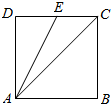 如图,正方形ABCD中,E为DC的中点,若$\overrightarrow{AE}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ的值为( )
如图,正方形ABCD中,E为DC的中点,若$\overrightarrow{AE}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ的值为( )| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=20,PB=10,∠BAC的角平分线与BC和圆O分别交于点D和E.
如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=20,PB=10,∠BAC的角平分线与BC和圆O分别交于点D和E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com