
 ,
,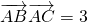 ,且
,且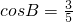 ,求cosC.
,求cosC. 解:(1)如图,在直角坐标系xOy内做单位圆O,并作出角α、β与-β,使角α的始边为Ox,交⊙O于点P1,终边交⊙O于P2;角β的始边为OP2,终边交⊙O于P3;角-β的始边为OP1,终边交⊙O于P4.
解:(1)如图,在直角坐标系xOy内做单位圆O,并作出角α、β与-β,使角α的始边为Ox,交⊙O于点P1,终边交⊙O于P2;角β的始边为OP2,终边交⊙O于P3;角-β的始边为OP1,终边交⊙O于P4. bcsinA=
bcsinA= >0,
>0, •
• =bccosA=3>0
=bccosA=3>0 ),cosA=3sinA
),cosA=3sinA ,cosA=
,cosA= …(10分)
…(10分) ,sinB=
,sinB= …(11分)
…(11分) ,
, …(14分)
…(14分) bcsinA=
bcsinA= >0,
>0, •
• =bccosA=3可求得sinA=
=bccosA=3可求得sinA= ,cosA=
,cosA= ,又cosB=
,又cosB= ,可求得sinB=
,可求得sinB= ,利用两角和的余弦即可求得cosC.
,利用两角和的余弦即可求得cosC.

科目:高中数学 来源: 题型:解答题
 ,证明:函数g(x)在(0,
,证明:函数g(x)在(0, )上单调递减.
)上单调递减.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 的左、右焦点分别为F1,F2,O为原点.
的左、右焦点分别为F1,F2,O为原点.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 ,设目标函数z=2x+y,若存在不同的三点(x,y)使目标函数z的值构成等比数列,则以下不可能成为公比的数是
,设目标函数z=2x+y,若存在不同的三点(x,y)使目标函数z的值构成等比数列,则以下不可能成为公比的数是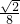


查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,经过点M(1,1)能否作一条直线l,使直线l与双曲线交于A、B,且M是线段AB的中点,若存在这样的直线l,求出它的方程;若不存在,说明理由.
,经过点M(1,1)能否作一条直线l,使直线l与双曲线交于A、B,且M是线段AB的中点,若存在这样的直线l,求出它的方程;若不存在,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com