
【题目】已知离心率为![]() 的椭圆
的椭圆![]() ,
,![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() ,斜率为1的直线
,斜率为1的直线![]() 经过
经过![]() 且与椭圆交于
且与椭圆交于![]() 两点.
两点.
(1)求![]() 面积;
面积;
(2)动直线![]() 与椭圆有且仅有一个交点,且与直线
与椭圆有且仅有一个交点,且与直线![]() ,
,![]() 分别交于
分别交于![]() 两点,且
两点,且![]() 为椭圆的右焦点,证明
为椭圆的右焦点,证明![]() 为定值.
为定值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由![]() 得出
得出![]() (0,1),结合椭圆离心率
(0,1),结合椭圆离心率![]() ,解得
,解得![]() ,即可得出椭圆标准方程
,即可得出椭圆标准方程![]() ,从而得出直线
,从而得出直线![]() 方,联立求出交点
方,联立求出交点![]() 和
和![]() 的坐标,利用两点间的距离公式求出
的坐标,利用两点间的距离公式求出![]() 和点到直线的距离求出
和点到直线的距离求出![]() ,即可得出
,即可得出![]() 的面积.
的面积.
(2)设直线![]() 方程为
方程为![]() ,联立直线
,联立直线![]() 和椭圆方程,得
和椭圆方程,得![]() ,根据
,根据![]() ,求得
,求得![]() ,从而求得
,从而求得![]() 坐标,利用两点间的距离求出
坐标,利用两点间的距离求出![]() 和
和![]() ,即可求得
,即可求得![]() ,
,
解:(1)由题意可知:抛物线![]() 的焦点坐标为:
的焦点坐标为:![]() (0,1),
(0,1),
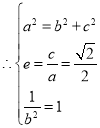 ,解得
,解得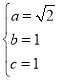 ,
,
![]() 椭圆方程为
椭圆方程为![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
联立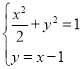 ,整理得
,整理得![]() ,
,
解得![]() ,
,![]() ,
,
则![]() (0,1),
(0,1),![]() ,
,
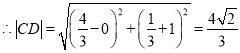 ,
,
原点到直线![]() 的距离
的距离![]() ,
,
![]() .
.
所以![]() 面积为
面积为![]() .
.
(2)由题可知,直线![]() 斜率存在,设直线
斜率存在,设直线![]() 方程为
方程为![]() ,
,
联立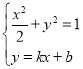 ,整理得
,整理得![]() ,
,
![]() 直线
直线![]() 与椭圆有且仅有一个交点,
与椭圆有且仅有一个交点,
![]()
![]() ,
,
整理得![]() ,
,
由题可得![]() ,
,![]() ,
,![]() ,
,
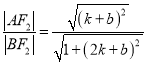
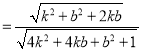
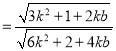 =
=![]() .
.
所以![]() 为定值
为定值![]() .
.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是梯形.BC∥AD,AB=BC=CD=1,AD=2,![]() ,
,![]()
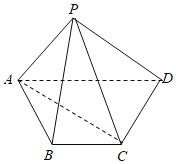
(Ⅰ)证明;AC⊥BP;
(Ⅱ)求直线AD与平面APC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,点
中,点![]() 、
、![]() 分别是棱
分别是棱![]() 和
和![]() 的中点,给出下列结论:
的中点,给出下列结论:
①直线![]() 与
与![]() 所成角为
所成角为![]() ;②正方体的所有棱中与直线
;②正方体的所有棱中与直线![]() 异面的有
异面的有![]() 条;③直线
条;③直线![]() 平面
平面![]() ;④平面
;④平面![]() 平面
平面![]() .其中正确的是( )
.其中正确的是( )
A.①②B.②③C.②④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的零点构成一个公差为
的零点构成一个公差为![]() 的等差数列,把函数
的等差数列,把函数![]() 的图象沿
的图象沿![]() 轴向右平移
轴向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.关于函数
的图象.关于函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
A. 在![]() 上是增函数B. 其图象关于直线
上是增函数B. 其图象关于直线![]() 对称
对称
C. 函数![]() 是偶函数D. 在区间
是偶函数D. 在区间![]() 上的值域为
上的值域为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·石家庄一模)祖暅是南北朝时期的伟大数学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖去一个圆锥所得的几何体,图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( )
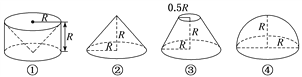
A. ①② B. ①③
C. ②④ D. ①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com