
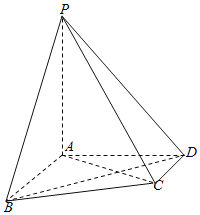
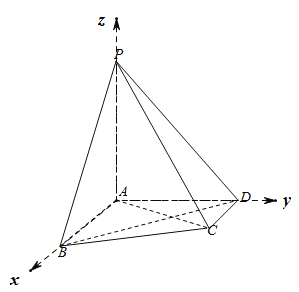
【题目】如图,在四棱锥P-ABCD中,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)证明:![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)设Q为线段PD上的点,且直线AQ和平面PAC所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,利用向量法能证明
轴,建立空间直角坐标系,利用向量法能证明![]() .
.
(2)求出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,利用向量法能求出二面角
的法向量,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
(3)设![]() 为线段
为线段![]() 上的点,
上的点,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求出
,求出![]() ,由平面
,由平面![]() 的法向量
的法向量![]() ,且直线
,且直线![]() 和平面
和平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,利用向量法能求出结果.
,利用向量法能求出结果.
解:(1)证明:∵在四棱锥![]() 中,
中,![]() 平面ABCD,
平面ABCD,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴以A为原点,AB为x轴,AD为y轴,AP为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
∴![]() ,∴
,∴![]() .
.
(2)解:![]() ,
,![]() ,
,![]() ,
,
设平面APC的法向量![]() ,
,
则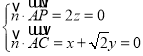 ,
,
取![]() ,得
,得![]() ,
,
平面PCD的法向量![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,
,
则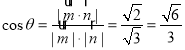 .
.
∴二面角![]() 的余弦值为
的余弦值为![]() .
.
(3)解:设Q为线段PD上的点,![]() ,
,
![]() ,
,![]()
则![]() ,
,
解得![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵平面PAC的法向量![]() ,
,
且直线AQ和平面PAC所成角的正弦值为![]() ,
,
∴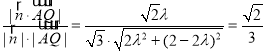 ,
,
解得![]() 或
或![]() (舍),
(舍),
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】新型冠状病毒最近在全国蔓延,具有很强的人与人之间的传染性,该病毒在进入人体后一般有14天的潜伏期,在这14天的潜伏期内患者无任何症状,为病毒传播的最佳时间.假设每位病毒携带者在潜伏期内每天有![]() 位密切接触者,接触病毒携带者后被感染的概率为
位密切接触者,接触病毒携带者后被感染的概率为![]() ,每位密切接触者不用再接触其他病毒携带者.
,每位密切接触者不用再接触其他病毒携带者.
(1)求一位病毒携带者一天内感染的人数![]() 的均值;
的均值;
(2)若![]() ,
,![]() 时,从被感染的第一天算起,试计算某一位病毒携带者在14天潜伏期内,被他平均累计感染的人数(用数字作答);
时,从被感染的第一天算起,试计算某一位病毒携带者在14天潜伏期内,被他平均累计感染的人数(用数字作答);
(3)3月16日20时18分,由我国军事科学院军事科学研究院陈薇院士领衔的科学团队,研制重组新型冠状病毒疫苗获批进入临床状态,新疫苗的使用,可以极大减少感染新型冠状病毒的人数,为保证安全性和有效性,某科研团队抽取500支新冠疫苗,观测其中某项质量指标值,得到如下频率分布直方图:
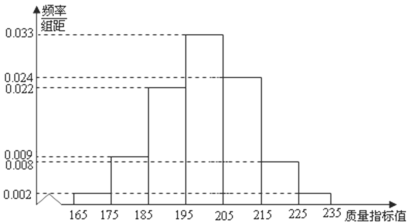
①求这500支该项质量指标值的样本平均值![]() (同一组的数据用该组区代表间的中点值)
(同一组的数据用该组区代表间的中点值)
②由直方图可以认为,新冠疫苗的该项质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算可得这500支新冠疫苗该项指标值的样本方差
,经计算可得这500支新冠疫苗该项指标值的样本方差![]() .现有5名志愿者参与临床试验,观测得出该项指标值分别为:206,178,195,160,229,试问新冠疫苗的该项指标值是否正常,为什么?
.现有5名志愿者参与临床试验,观测得出该项指标值分别为:206,178,195,160,229,试问新冠疫苗的该项指标值是否正常,为什么?
参考数据:![]() ,若
,若![]()
![]() ,则
,则![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为提高服务质量,随机调查了60名男顾客和80名女顾客,每位顾客均对该商场的服务给出满意或不满意的评价,得到下面不完整的列联表:
满意 | 不满意 | 合计 | |
男顾客 | 50 | ||
女顾客 | 50 | ||
合计 |
(1)根据已知条件将列联表补充完整;
(2)能否有![]() 的把握认为男、女顾客对该商场服务的评价有差异?
的把握认为男、女顾客对该商场服务的评价有差异?
附: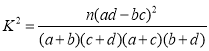
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面中,△ABC的两个顶点A、B的坐标分别为A(﹣1,0),B (1,0),平面内两点G、M同时满足下列条件:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ∥
∥![]() ,则△ABC的顶点C的轨迹方程为_____.
,则△ABC的顶点C的轨迹方程为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为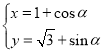 (α为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(α为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() ,(
,(![]() ).
).
(1)求曲线C的极坐标方程;
(2)设直线l与曲线C相交于不同的两点![]() ,
,![]() ,指出
,指出![]() 的范围,并求
的范围,并求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为该椭圆的一条垂直于
为该椭圆的一条垂直于![]() 轴的动弦,直线
轴的动弦,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
(1)证明:点![]() 恒在椭圆
恒在椭圆![]() 上.
上.
(2)设直线![]() 与椭圆
与椭圆![]() 只有一个公共点
只有一个公共点![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,在平面内是否存在定点
,在平面内是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出该点坐标;若不存在,说明理由.
恒成立?若存在,求出该点坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过双曲线C:![]() 1(a>0,b>0)右焦点F2作双曲线一条渐近线的垂线,垂足为P,与双曲线交于点A,若
1(a>0,b>0)右焦点F2作双曲线一条渐近线的垂线,垂足为P,与双曲线交于点A,若![]() ,则双曲线C的渐近线方程为( )
,则双曲线C的渐近线方程为( )
A.y=±![]() xB.y=±xC.y=±2xD.y=±
xB.y=±xC.y=±2xD.y=±![]() x
x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com