
【题目】已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,且
,且![]() 在椭圆
在椭圆![]() 上运动,当点
上运动,当点![]() 恰好在直线l:
恰好在直线l:![]() 上时,
上时,![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)作与![]() 平行的直线
平行的直线![]() ,与椭圆交于
,与椭圆交于![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() ,若
,若![]() 的斜率分别为
的斜率分别为![]() ,求
,求![]() 的取值范围.
的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】2019年国庆节假期期间,某商场为掌握假期期间顾客购买商品人次,统计了10月1日7:00-23:00这一时间段内顾客0这一时间段内顾客购买商品人次,统计发现这一时间段内顾客购买商品共5000人次顾客购买商品时刻的频率分布直方图如下图所示,其中时间段7:00 11:00,11:00 15:00,15:00 ~19:00,19:00~23:00,依次记作[7,11),[11,15),[15,19),[19,23].
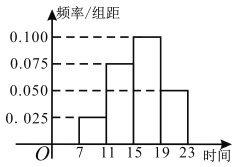
(1)求该天顾客购买商品时刻的中位数t与平均值![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)现从10月1日在该商场购买商品的顾客中随机抽取100名顾客,经统计有男顾客 40人,其中10人购物时刻在[19,23](夜晚),女顾客60人,其中50人购物时刻在[7,19)(白天),根据提供的统计数据,完成下面的2×2列联表,并判断是否有90%的把握认为“男顾客更喜欢在夜晚购物”?
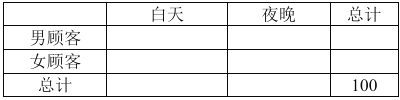
附:![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国在贵州省平塘县境内修建的500米口径球面射电望远镜(FAST)是目前世界上最大单口径射电望远镜.使用三年来,已发现132颗优质的脉冲星候选体,其中有93颗已被确认为新发现的脉冲星,脉冲星是上世纪60年代天文学的四大发现之一,脉冲星就是正在快速自转的中子星,每一颗脉冲星每两脉冲间隔时间(脉冲星的自转周期)是-定的,最小小到0.0014秒,最长的也不过11.765735秒.某-天文研究机构观测并统计了93颗已被确认为新发现的脉冲星的自转周期,绘制了如图的频率分布直方图.

(1)在93颗新发现的脉冲星中,自转周期在2至10秒的大约有多少颗?
(2)根据频率分布直方图,求新发现脉冲星自转周期的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角![]() 中,
中,![]() ,
,![]() 通过
通过![]() 以直线
以直线![]() 为轴顺时针旋转
为轴顺时针旋转![]() 得到(
得到(![]() ).点
).点![]() 为斜边
为斜边![]() 上一点.点
上一点.点![]() 为线段
为线段![]() 上一点,且
上一点,且![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)当直线![]() 与平面
与平面![]() 所成的角取最大值时,求二面角
所成的角取最大值时,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学的对称美在中国传统文化中多有体现,譬如如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的和谐美.如果能够将圆的周长和面积同时平分的函数称为这个圆的“优美函数“,下列说法错误的是( )

A.对于任意一个圆,其“优美函数“有无数个
B.![]() 可以是某个圆的“优美函数”
可以是某个圆的“优美函数”
C.正弦函数![]() 可以同时是无数个圆的“优美函数”
可以同时是无数个圆的“优美函数”
D.函数![]() 是“优美函数”的充要条件为函数
是“优美函数”的充要条件为函数![]() 的图象是中心对称图形
的图象是中心对称图形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com