
已知无穷数列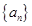 的前
的前 项和为
项和为 ,且满足
,且满足 ,其中
,其中 、
、 、
、 是常数.
是常数.
(1)若 ,
, ,
, ,求数列
,求数列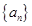 的通项公式;
的通项公式;
(2)若 ,
, ,
, ,且
,且 ,求数列
,求数列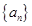 的前
的前 项和
项和 ;
;
(3)试探究 、
、 、
、 满足什么条件时,数列
满足什么条件时,数列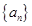 是公比不为
是公比不为 的等比数列.
的等比数列.
(1) ;(2)
;(2)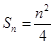 ;(3)
;(3) ,
,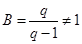 或
或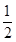 或
或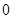 ,
, .
.
解析试题分析:(1)已知 与
与 的关系,要求
的关系,要求 ,一般是利用它们之间的关系
,一般是利用它们之间的关系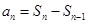
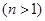 ,把
,把 ,化为
,化为 ,得出数列
,得出数列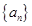 的递推关系,从而求得通项公式
的递推关系,从而求得通项公式 ;(2)与(1)类似,先求出
;(2)与(1)类似,先求出 ,
, 时,推导出
时,推导出 与
与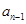 之间的关系,求出通项公式,再求出前
之间的关系,求出通项公式,再求出前 项和
项和 ;(3)这是一类探究性命题,可假设结论成立,然后由这个假设的结论来推导出条件,本题设数列
;(3)这是一类探究性命题,可假设结论成立,然后由这个假设的结论来推导出条件,本题设数列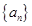 是公比不为
是公比不为 的等比数列,则
的等比数列,则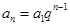 ,
,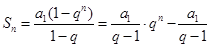 ,代入恒成立的等式
,代入恒成立的等式 ,得
,得 对于一切正整数
对于一切正整数 都成立,所以
都成立,所以 ,
, ,
,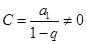 ,得出这个结论之后,还要反过来,由这个条件证明数列
,得出这个结论之后,还要反过来,由这个条件证明数列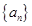 是公比不为
是公比不为 的等比数列,才能说明这个结论是正确的.在讨论过程中,还要讨论
的等比数列,才能说明这个结论是正确的.在讨论过程中,还要讨论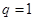 的情况,因为
的情况,因为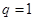 时,
时,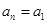 ,
,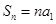 ,当然这种情况下,
,当然这种情况下,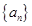 不是等比数列,另外
不是等比数列,另外
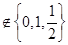 .
.
试题解析:(1)由 ,得
,得 ; 1分
; 1分
当 时,
时,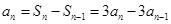 ,即
,即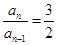 2分
2分
所以 ; 1分
; 1分
(2)由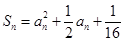 ,得
,得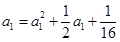 ,进而
,进而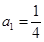 , 1分
, 1分
当 时,
时,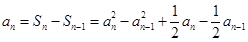
得 ,
,
因为 ,所以
,所以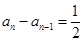 , 2分
, 2分
进而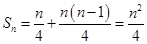 2分
2分
(3)若数列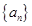 是公比为
是公比为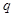 的等比数列,
的等比数列,
①当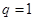 时,
时,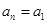 ,
,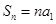
由 ,得
,得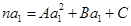 恒成立.
恒成立.
所以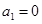 ,与数列
,与数列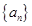 是等比数列矛盾; 1分
是等比数列矛盾; 1分
②当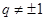 ,
,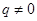 时,
时,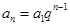 ,
,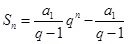 , 1分
, 1分
由 恒成立,
恒成立,
得 对于一切正整数
对于一切正整数 都成立
都成立
所以 ,
,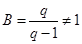 或
或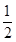 或
或

科目:高中数学 来源: 题型:解答题
在等差数列{an}中,a16+a17+a18=a9=-36,其前n项和为Sn.
(1)求Sn的最小值,并求出Sn取最小值时n的值;
(2)求Tn=|a1|+|a2|+…+|an|.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列 中,
中, ,
, ,
, .
.
(1)证明:数列 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;
(2)在数列 中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
(3)若 且
且 ,
, ,求证:使得
,求证:使得 ,
, ,
, 成等差数列的点列
成等差数列的点列 在某一直线上.
在某一直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com