
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),将曲线
为参数),将曲线![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() ,在以原点为极点,
,在以原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)说明曲线![]() 是哪一种曲线,并将曲线
是哪一种曲线,并将曲线![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上的任意一点,求点
上的任意一点,求点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
【答案】(1)曲线![]() 以原点为圆心,半径为
以原点为圆心,半径为![]() 的圆;
的圆;![]()
(2)![]()
【解析】
(1)曲线![]() 的参数方程
的参数方程![]() ,
,![]() 的参数方程消去参数
的参数方程消去参数![]() ,能求出
,能求出![]() 的普通方程,
的普通方程,![]() 以原点为圆心,半径为
以原点为圆心,半径为![]() 的圆,由此能求出
的圆,由此能求出![]() 的极坐标方程.
的极坐标方程.
(2)解法一:直线![]() 的普通方程为
的普通方程为![]() ,由圆
,由圆![]() 的半径为
的半径为![]() ,且圆心到直线的距离
,且圆心到直线的距离![]() ,从而圆
,从而圆![]() 与直线
与直线![]() 相离,由此能求出点
相离,由此能求出点![]() 到直线
到直线![]() 的距离的最小值;解法二:由直线的极坐标方程求出直线
的距离的最小值;解法二:由直线的极坐标方程求出直线![]() 的普通方程为
的普通方程为![]() ,曲线
,曲线![]() 上的点
上的点![]() 到直线
到直线![]() 的距离
的距离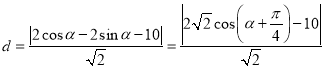 ,由此能求出点
,由此能求出点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
(1)![]() 曲线
曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),
为参数),
将曲线![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() ,
,
![]() 曲线
曲线![]() 的参数方程
的参数方程![]() ,
,
![]()
![]() 的参数方程消去参数
的参数方程消去参数![]() ,
,
所以![]() 的普通方程为
的普通方程为![]() ,
,
![]() 曲线
曲线![]() 以原点为圆心,半径为
以原点为圆心,半径为![]() 的圆,
的圆,
![]()
![]() 的极坐标为
的极坐标为![]() ,即
,即![]() .
.
(2)解法一:![]() 直线
直线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
![]() 直线
直线![]() 的普通方程为
的普通方程为![]() ,
,
因为圆![]() 的半径为
的半径为![]() ,且圆心到直线
,且圆心到直线![]() 的距离
的距离![]() ,
,
因为![]() ,所以圆
,所以圆![]() 与直线
与直线![]() 相离,
相离,
所以圆![]() 上的点
上的点![]() 到直线
到直线![]() 的距离的最小值
的距离的最小值![]() .
.
解法二:由直线的极坐标方程为![]()
则直线![]() 的普通方程为
的普通方程为![]() ,
,
曲线![]() 上的点
上的点![]() 到直线
到直线![]() 的距离
的距离
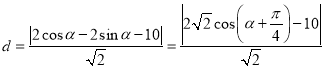 ,
,
当![]() 时,即
时,即![]() 时,
时,
![]() 取得最小值为
取得最小值为 .
.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】绿水青山就是金山银山.某山村为做好水土保持,退耕还林,在本村的山坡上种植水果,并推出山村游等旅游项目.为预估今年7月份游客购买水果的情况,随机抽样统计了去年7月份100名游客的购买金额.分组如下:![]() ,
,![]() ,
,![]()
![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
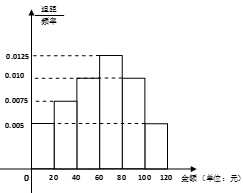
(1)请用抽样的数据估计今年7月份游客人均购买水果的金额(同一组中的数据用该组区间中点作代表).
(2)若把去年7月份购买水果不低于80元的游客,称为“水果达人”. 填写下面列联表,并根据列联表判断是否有95%的把握认为“水果达人”与性别有关系?
水果达人 | 非水果达人 | 合计 | |
男 | 10 | ||
女 | 30 | ||
合计 |
(3)为吸引顾客,商家特推出两种促销方案.方案一:每满80元可立减10元;方案二:金额超过80元可抽奖三次,每次中奖的概率为![]() ,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.若每斤水果10元,你打算购买12斤水果,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.若每斤水果10元,你打算购买12斤水果,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
附:参考公式和数据:![]() ,
,![]() .临界值表:
.临界值表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为 为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=asinθ(a≠0).
为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=asinθ(a≠0).
(1)求圆C的直角坐标方程与直线l的普通方程;
(2)设直线l截圆C的弦长是半径长的![]() 倍,求a的值.
倍,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() 是
是![]() 边上异于端点的动点,
边上异于端点的动点,![]() 于点
于点![]() ,将矩形
,将矩形![]() 沿
沿![]() 折叠至
折叠至![]() 处,使面
处,使面![]() 面
面![]() .点
.点![]() 分别为
分别为![]() 的中点.
的中点.
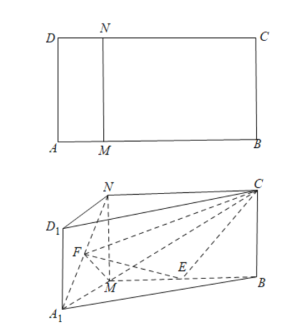
(1)证明:![]() //面
//面![]() ;
;
(2)设![]() ,当x为何值时,四面体
,当x为何值时,四面体![]() 的体积最大,并求出最大值.
的体积最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,北京2022年冬奥组委会启动志愿者全球招募,仅一个月内报名人数便突破60万,其中青年学生约有50万人.现从这50万青年学生志愿者中,按男女分层抽样随机选取20人进行英语水平测试,所得成绩(单位:分)统计结果用茎叶图记录如下:
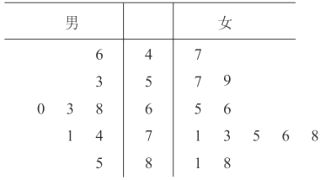
(Ⅰ)试估计在这50万青年学生志愿者中,英语测试成绩在80分以上的女生人数;
(Ⅱ)从选出的8名男生中随机抽取2人,记其中测试成绩在70分以上的人数为X,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)为便于联络,现将所有的青年学生志愿者随机分成若干组(每组人数不少于5000),并在每组中随机选取![]() 个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出
个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出![]() 的最小值.(结论不要求证明)
的最小值.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)和y=g(x)在[-2,2]的图像如图所示,给出下列四个命题:

①方程f[g(x)]=0有且仅有6个根
②方程g[f(x)]=0有且仅有3个根
③方程f[f(x)]=0有且仅有5个根
④方程g[g(x)]=0有且仅有4个根
其中正确的命题是___
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种“笼具”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为![]() ,高为
,高为![]() ,圆锥的母线长为
,圆锥的母线长为![]() .
.
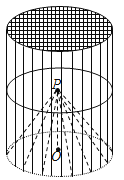
(1)求这种“笼具”的体积(结果精确到0.1![]() );
);
(2)现要使用一种纱网材料制作50个“笼具”,该材料的造价为每平方米8元,共需多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com