
已知点P(x,y)对应的复数z满足![]() , 则点Q(x+y,xy)的轨迹是 ( ).
, 则点Q(x+y,xy)的轨迹是 ( ).
A. 圆 B. 抛物线的一部分 C. 椭圆 D. 双曲线的一部
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
| x2 |
| 4 |
| 2 |
| |PF2|+|QF2| |
| |PF2|•|QF2| |
| ||
| 2 |
| 1 |
| 2 |
| PA |
| PF2 |
| 7 |
| 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| f(x2)-f(x1) |
| x2-x1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 上一点,F1、F2为椭圆左、右焦点,下列结论中:①△PF1F2面积的最大值为
上一点,F1、F2为椭圆左、右焦点,下列结论中:①△PF1F2面积的最大值为 ;②若过点P、F2的直线l与椭圆的另一交点为Q,则△PF1Q的周长为8;③若过点P、F2的直线l与椭圆的另一交点为Q,则恒有
;②若过点P、F2的直线l与椭圆的另一交点为Q,则△PF1Q的周长为8;③若过点P、F2的直线l与椭圆的另一交点为Q,则恒有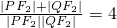 ;对定点
;对定点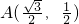 ,则
,则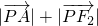 的取值范围为
的取值范围为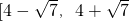 .其中正确结论的番号是________.
.其中正确结论的番号是________.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| x2 |
| 4 |
| 2 |
| |PF2|+|QF2| |
| |PF2|•|QF2| |
| ||
| 2 |
| 1 |
| 2 |
| PA |
| PF2 |
| 7 |
| 7 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省镇江市扬中二中高三(上)期末数学模拟试卷(解析版) 题型:解答题
 ”.类比这一结论,我们猜想:“若曲线C的方程为
”.类比这一结论,我们猜想:“若曲线C的方程为 (如图),则xE•xF也是与点M、N、P位置无关的定值”,请你对该猜想给出证明.
(如图),则xE•xF也是与点M、N、P位置无关的定值”,请你对该猜想给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com