
【题目】在50和350之间所有末位数是1的整数之和是( )
A. 5880 B. 5539 C. 5208 D. 4877
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mln(x+1),g(x)= ![]() (x>﹣1). (Ⅰ)讨论函数F(x)=f(x)﹣g(x)在(﹣1,+∞)上的单调性;
(x>﹣1). (Ⅰ)讨论函数F(x)=f(x)﹣g(x)在(﹣1,+∞)上的单调性;
(Ⅱ)若y=f(x)与y=g(x)的图象有且仅有一条公切线,试求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司按现有能力,每月收入为70万元,公司分析部门测算,若不进行改革,入世后因竞争加剧收入将逐月减少.分析测算得入世第一个月收入将减少3万元,以后逐月多减少2万元,如果进行改革,即投入技术改造300万元,且入世后每月再投入1万元进行员工培训,则测算得自入世后第一个月起累计收入![]() 与时间
与时间![]() (以月为单位)的关系为
(以月为单位)的关系为![]() ,且入世第一个月时收入将为90万元,第二个月时累计收入为170万元,问入世后经过几个月,该公司改革后的累计纯收入高于不改革时的累计纯收入.
,且入世第一个月时收入将为90万元,第二个月时累计收入为170万元,问入世后经过几个月,该公司改革后的累计纯收入高于不改革时的累计纯收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)(2)两个班联合开展“诗词大会进校园,国学经典润心田”古诗词竞赛主题班会活动,主持人从这两个班分别随机选出20名同学进行当场测试,他们的测试成绩按[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)分组,分别用频率分布直方图与茎叶图统计如图(单位:分): 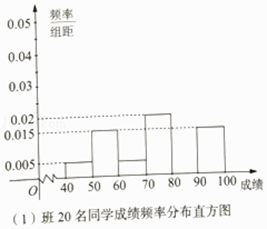
高一(2)班20名学生成绩茎叶图:
4 | 5 |
5 | 2 |
6 | 4 5 6 8 |
7 | 0 5 5 8 8 8 8 9 |
8 | 0 0 5 5 |
9 | 4 5 |
(Ⅰ)分别计算两个班这20名同学的测试成绩在[80,90)的频率,并补全频率分布直方图;
(Ⅱ)分别从两个班随机选取1人,设这两人中成绩在[80,90)的人数为X,求X的分布列(频率当作概率使用).
(Ⅲ)运用所学统计知识分析比较两个班学生的古诗词水平.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P1(x1 , y1),P2(x2 , y2),P3(x3 , y3),P4(x4 , y4),P5(x5 , y5),P6(x6 , y6)是抛物线C:y2=2px(p>0)上的点,F是抛物线C的焦点,若|P1F|+|P2F|+|P3F|+|P4F|+|P5F|+|P6F|=36,且x1+x2+x3+x4+x5+x6=24,则抛物线C的方程为( )
A.y2=4x
B.y2=8x
C.y2=12x
D.y2=16x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具所需成本费用为P元,且P=1 000+5x+![]() x2,而每套售出的价格为Q元,其中Q(x)=a+
x2,而每套售出的价格为Q元,其中Q(x)=a+![]() (a,b∈R),
(a,b∈R),
(1)问:玩具厂生产多少套时,使得每套所需成本费用最少?
(2)若生产出的玩具能全部售出,且当产量为150套时利润最大,此时每套价格为30元,求a,b的值.(利润=销售收入-成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定实数 t,已知命题 p:函数![]() 有零点;命题 q: x∈[1,+∞)
有零点;命题 q: x∈[1,+∞) ![]() ≤4
≤4![]() -1.
-1.
(Ⅰ)当 t=1 时,判断命题 q 的真假;
(Ⅱ)若 p∨q 为假命题,求 t 的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年入冬以来,各地雾霾天气频发,![]() 频频爆表(
频频爆表(![]() 是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与
是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与![]() 的浓度是否相关,某市现采集周一到周五某一时间段车流量与
的浓度是否相关,某市现采集周一到周五某一时间段车流量与![]() 的数据如下表:
的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 50 | 51 | 54 | 57 | 58 |
| 69 | 70 | 74 | 78 | 79 |
(1)请根据上述数据,在下面给出的坐标系中画出散点图;

(2)试判断![]() 与
与![]() 是否具有线性关系,若有请求出
是否具有线性关系,若有请求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,若没有,请说明理由;
,若没有,请说明理由;
(3)若周六同一时间段的车流量为60万辆,试根据(2)得出的结论,预报该时间段的![]() 的浓度(保留整数).
的浓度(保留整数).
参考公式:
 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.设p:f(x)=x3+2x2+mx+1是R上的单调增函数, ![]() ,则p是q的必要不充分条件
,则p是q的必要不充分条件
B.若命题 ![]() ,则¬p:?x∈R,x2﹣x+1>0
,则¬p:?x∈R,x2﹣x+1>0
C.奇函数f(x)定义域为R,且f(x﹣1)=﹣f(x),那么f(8)=0
D.命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0,则x2+y2≠0”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com