
【题目】已知曲线![]() 的一个最高点为
的一个最高点为![]() ,与点
,与点![]() 相邻一个最低点为
相邻一个最低点为![]() ,直线
,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的单调增区间;
的单调增区间;
(3)若![]() 时,函数
时,函数![]() 恰有一个零点,求实数
恰有一个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据最高点坐标,可得![]() ;由最高点和最低点连线与
;由最高点和最低点连线与![]() 轴的交点可求得周期,进而得
轴的交点可求得周期,进而得![]() .将最高点坐标代入解析式,结合
.将最高点坐标代入解析式,结合![]() 的取值范围,即可求得函数
的取值范围,即可求得函数![]() 的解析式;
的解析式;
(2)由(1)可得函数![]() 的解析式,由余弦函数的图像与性质即可求得函数
的解析式,由余弦函数的图像与性质即可求得函数![]() 的单调增区间.
的单调增区间.
(3)代入解析式,分离参数可得![]() .根据
.根据![]() 方程只有一个根,求得
方程只有一个根,求得![]() 的值域,即可求得
的值域,即可求得![]() 的取值范围.
的取值范围.
(1)由题知最高点![]() ,所以
,所以![]() ,
,
最高点和最低点连线与![]() 轴的交点
轴的交点![]() 可得
可得![]() ,则
,则![]() ;
;
则![]()
由最高点坐标![]() 可知
可知![]() ,
,![]()
解得![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() .
.
所以![]() .
.
(2)由(1)可知![]()
函数![]() 的单调增区间,由余弦函数的图像与性质可知
的单调增区间,由余弦函数的图像与性质可知![]() ,
,![]()
解得![]() ,
,![]() ,
,
所以![]() 单调递增区间为
单调递增区间为![]() .
.
(3)![]()
变形可得![]()
即![]() 在
在![]() 上只有一个根.
上只有一个根.
因为![]() ,所以
,所以![]() .
.
则
所以![]() ,
,![]() 或
或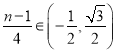 ,
,
所以![]() 的取值集合为:
的取值集合为:![]() .
.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
【题目】最近上映的电影《后来的我们》引起了一阵热潮,为了了解大众对这部电影的评价,随机访问了50名观影者,根据这50人对该电影的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]() ,
,![]() ,…,
,…,![]() ,
,![]() .
.

(1)求频率分布直方图中![]() 的值,并估计观影者对该电影评分不低于80的概率;
的值,并估计观影者对该电影评分不低于80的概率;
(2)由频率分布直方图估计评分的中位数(保留两位小数)与平均数;
(3)从评分在![]() 的观影者中随机抽取2人,求至少有一人评分在
的观影者中随机抽取2人,求至少有一人评分在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() .以极点为平面直角坐标系的原点,极轴为
.以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(Ⅰ)将曲线![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角
的倾斜角![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台有一档益智答题类综艺节日,每期节目从现场编号为01~80的80名观众中随机抽取10人答题.答题选手要从“科技”和“文艺”两类题目中选一类作答,一共回答10个问题,答对1题得1分.
(1)若采用随机数表法抽取答题选手,按照以下随机数表,从下方带点的数字2开始向右读,每次读取两位数,一行用完接下一行左端,求抽取的第6个观众的编号.
1622779439 4954435482 1737932378 8735![]() 09643 8426349164
09643 8426349164
8442175331 5724550688 7704744767 2176335025 8392120676
(2)若采用等距系统抽样法抽取答题选手,且抽取的最小编号为06,求抽取的最大编号.
(3)某期节目的10名答题选手中6人选科技类题目,4人选文艺类题目.其中选择科技类的6人得分的平均数为7,方差为![]() ;选择文艺类的4人得分的平均数为8,方差为
;选择文艺类的4人得分的平均数为8,方差为![]() .求这期节目的10名答题选手得分的平均数和方差.
.求这期节目的10名答题选手得分的平均数和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,且Sn=2an﹣2(n∈N*),数列{bn}满足bn=(2n﹣1)an,数列{bn}的前n项和Tn(n∈N*),
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和Tn;
(3)求![]() 的最小值以及取得最小值时n的值.
的最小值以及取得最小值时n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com