
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
| 1 |
| 6 |
| 1 |
| 2 |
| 4 |
| 3 |
| 3 |
| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| n(n+1)(2n+1) |
| 6 |
| n(n+1)(n+2)(an+b) |
| 12 |
查看答案和解析>>
科目:高中数学 来源:2010-2011年辽宁省东北育才学校高二下学期期中考试文科数学 题型:解答题
(本小题满分12分)
关于 的函数
的函数 与数列
与数列 具有关系:
具有关系: , (
, ( 为常数),
为常数),
 (
( =1,2,3,…),又已知函数
=1,2,3,…),又已知函数 的导数
的导数 ,
, 为方程
为方程 的实根.
的实根.
(I)用数学归纳法证明: ;
;
(II)证明: .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011年辽宁省高二下学期期中考试理科数学 题型:解答题
(本小题满分12分)
关于 的函数
的函数 与数列
与数列 具有关系:
具有关系:
 ,
, (
( =1,2,3,…)(
=1,2,3,…)(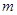 为常数),又设函数
为常数),又设函数 的导数
的导数 ,
,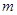 为方程
为方程 的实根.
的实根.
(I)用数学归纳法证明: ;
;
(II)证明: .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com