
【题目】已知圆心为![]() 的圆过原点
的圆过原点![]() ,且直线
,且直线![]() 与圆
与圆![]() 相切于点
相切于点![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)已知过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,且直线
,且直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点.
两点.
①若![]() ,求弦
,求弦![]() 的长;
的长;
②若圆![]() 上存在点
上存在点![]() ,使得
,使得![]() 成立,求直线
成立,求直线![]() 的斜率
的斜率![]() .
.
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC—A1B1C1中,∠ACB=90°,AC=AA1=1,![]() , AB1与A1B相交于点D,M为B1C1的中点 .
, AB1与A1B相交于点D,M为B1C1的中点 .

(1)求证:CD⊥平面BDM;
(2)求平面B1BD与平面CBD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 在区间
在区间![]() 上单调递增,在区间
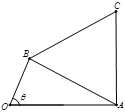
上单调递增,在区间![]() 上单调递减;如图,四边形
上单调递减;如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的内角
的内角![]() 的对边,
的对边,
且满足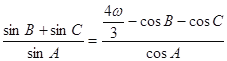 .
.
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]() ,设
,设![]() ,
,![]() ,
,
![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过坐标原点的直线l与圆C:x2+y2﹣8x+12=0相交于不同的两点A,B.
(1)求线段AB的中点P的轨迹M的方程.
(2)是否存在实数k,使得直线l1:y=k(x﹣5)与曲线M有且仅有一个交点?若存在,求出k的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
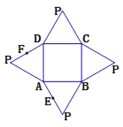
【题目】如图是一个几何体的平面展开图,其中四边形![]() 为正方形,
为正方形,![]() ,
,![]() ,
,![]() ,
,![]() 为全等的等边三角形,
为全等的等边三角形,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,在此几何体中,下列结论中正确的个数有()
的中点,在此几何体中,下列结论中正确的个数有()
①平面![]() 平面
平面![]()
②直线![]() 与直线
与直线![]() 是异面直线
是异面直线
③直线![]() 与直线
与直线![]() 共面
共面
④面![]() 与面
与面![]() 的交线与
的交线与![]() 平行
平行
A. 3B. 2C. 1D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两次购买同一种物品,可以用两种不同的策略,第一种是不考虑物品价格的升降,每次购买这种物品的数量一定;第二种是不考虑物品价格的升降,每次购买这种物品所花的钱数一定.哪种购物方式比较经济?你能把所得结论作一些推广吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学将100名高一新生分成水平相同的甲、乙两个平行班,每班50人,某教师采用![]() 、
、![]() 两种不同的教学模式分别在甲、乙两个班进行教改实验,为了了解教学效果,期末考试后,该教师分别从两班中各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示,记成绩不低于90分为“成绩优秀”.
两种不同的教学模式分别在甲、乙两个班进行教改实验,为了了解教学效果,期末考试后,该教师分别从两班中各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示,记成绩不低于90分为“成绩优秀”.

(1)在乙班的20个个体中,从不低于86分的成绩中随机抽取2人,求抽出的两个人均“成绩优秀”的概率;
(2)由以上统计数据填写![]() 列联表;能否在犯错误的概率不超过0.10的前提下认为成绩优秀与教学模型有关.
列联表;能否在犯错误的概率不超过0.10的前提下认为成绩优秀与教学模型有关.
甲班( | 乙班( | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.847 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.
(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E﹣BCD的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次文艺汇演,要将A、B、C、D、E、F这六个不同节目编排成节目单,如下表:

如果A、B两个节目要相邻,且都不排在第3号位置,则节目单上不同的排序方式有( )种
A. 192 B. 144 C. 96 D. 72
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com