在△
中，
、
、
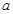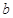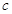分别为内角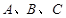
的对边，且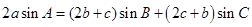
.
（1）求
的大小；（5分）
（2）若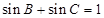
，判断△的形状.（7分）
（1）
；（2）顶角为钝角的等腰三角形.
解析试题分析：（1）求的大小，首先要从条件出发，条件是一个含有边、角混杂的等式，处理它必须归一，观察等式的特点，运用正弦定理化归为边比较简便，然后再考虑运用余弦定理，即可求出角的大小；（2）三角形形状的判断，要么从边考虑，要么从角考虑，通常从角考虑的情形多于从边考虑的情形，此题结合条件和（1）的结论，应从角考虑比较可行，在解三角形问题时，关键是适时用好边角互化及边角归一思想.
试题解析：（1）由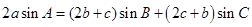结合正弦定理得：
，
即
，
，
，
. 5分
（2）由（1）知
，
，∴△是等腰三角形. 12分
考点：1.三角变换；2.解三角形；3.边角互化与边角归一的思想.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，且A，B，C成等差数列。
，
，求△ABC的面积；
成等比数列，试判断△ABC的形状。
．
中，
，
的值；
的长
，
，
，求B及S
.
中，角
所对的边分别为
，已知
,
，
．
的值；
的值.
中，内角
，
，
所对的边分别为
，
，
，已知
.
，
，求
．
中，设角
的对边分别为
，若
，
， 
，则
_____．
▲ ．