解(Ⅰ)由题意知,a
mn=1+(n-1)d
m.
a
2n-a
1n=[1+(n-1)d
2]-[1+(n-1)d
1]=(n-1)(d
2-d
1),同理,a
3n-a
2n=(n-1)(d
3-d
2),a
4n-a
3n=(n-1)(d
4-d
3),,a
nn-a
(n-1)n=(n-1)(d
n-d
n-1).a
1n,a
2n,a
3n,,a
nn成等差数列,
所以a
2n-a
1n=a
3n-a
2n=…=a
nn-a
(n-1)n,
故d
2-d
1=d
3-d
2=…=d
n-d
n-1.
即{d
n}是公差是d
2-d
1=3-1=2的等差数列.
所以,d
m=2m-1(3≤m≤n,m,n∈N
*).
(Ⅱ)由(Ⅰ)知d
m=2m-1(m∈N
*).
数列d
m分组如下:(1),(3,5,7),(9,11,13,15,17),…
按分组规律,第m组中有2m-1个奇数,
所以第1组到第m组共有1+3+5+…+(2m-1)=m
2个奇数.
注意到前k个奇数的和为1+3+5+…+(2k-1)=k
2,
所以前m
2个奇数的和为(m
2)
2=m
4,即前m组中所有数之和为m
4,
所以(c
m)
4=m
4.
因为c
m>0,所以c
m=m,从而
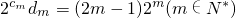
.
所以S
n=1•2+3•2
2+5•2
3+7•2
4+…+(2n-3)•2
n-1+(2n-1)•2
n.2S
n
=1•2
2+3•2
3+5•2
4+…+(2n-3)•2
n+(2n-1)•2
n+1,
故-S
n=2+2•2
2+2•2
3+2•2
4+…+2•2
n-(2n-1)•2
n+1
=2(2+2
2+2
3+…+2
n)-2-(2n-1)•2
n+1
=
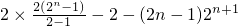
=(3-2n)2
n+1-6,
所以S
n=(2n-3)2
n+1+6.
(Ⅲ)由(Ⅱ)得d
n=2n-1(n∈N
*),S
n=(2n-3)2
n+1+6(n∈N
*).
故不等式
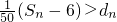
就是(2n-3)2
n+1>50(2n-1).
考虑函数f(n)=(2n-3)2
n+1-50(2n-1)=(2n-3)(2
n+1-50)-100.
当n=1,2,3,4,5时,都有f(n)<0,
即(2n-3)2
n+1<50(2n-1).
而f(6)=9(128-50)-100=602>0,
注意到当n≥6时,f(n)单调递增,故有f(n)>0.
因此当n≥6时,(2n-3)2
n+1>50(2n-1)成立,
即
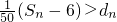
成立.
所以满足条件的所有正整数N=5,6,7,20.
分析:(Ⅰ)先根据首项和公差写出数列的通项公式,利用通项公式表示出数列a
1n,a
2n,a
3n,…,a
nn中的第2项减第1项,第4项减第3项,…,第n项减第n-1项,由此数列也为等差数列,得到表示出的差都相等,进而得到d
n是首项d
1,公差为d
2-d
1的等差数列,根据等差数列的通项公式即可求出{d
m}的通项;
(Ⅱ)由d
1=1,d
2=3,代入d
m中,确定出d
m的通项,根据题意的分组规律,得到第m组中有2m-1个奇数,所以得到第1组到第m组共有从1加到2m-1个奇数,利用等差数列的前n项和公式表示出之和,从而表示出前m
2个奇数的和,又前m组中所有数之和为(c
m)
4(c
m>0),即可得到c
m=m,代入
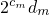
中确定出数列
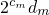
的通项公式,根据通项公式列举出数列
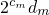
的前n项和S
n,记作①,两边乘以2得到另一个关系式,记作②,②-①即可得到前n项和S
n的通项公式;
(Ⅲ)由(Ⅱ)得到d
n和S
n的通项公式代入已知的不等式中,右边的式子移项到左边,合并化简后左边设成一个函数f(n),然后分别把n=1,2,3,4,5代入发现其值小于0,当n≥6时,其值大于0即原不等式成立,又N不超过20,所以得到满足题意的所有正整数N从5开始到20的连续的正整数.
点评:此题考查学生灵活运用等差数列的通项公式及前n项和公式化简求值,会利用错位相减的方法求数列的通项公式,考查了利用函数的思想解决实际问题的能力及运算能力,是一道中档题.

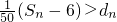 成立的所有N的值.
成立的所有N的值.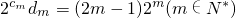 .
.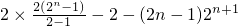 =(3-2n)2n+1-6,
=(3-2n)2n+1-6,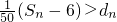 就是(2n-3)2n+1>50(2n-1).
就是(2n-3)2n+1>50(2n-1).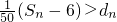 成立.
成立.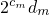 中确定出数列
中确定出数列 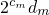 的通项公式,根据通项公式列举出数列
的通项公式,根据通项公式列举出数列 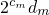 的前n项和Sn,记作①,两边乘以2得到另一个关系式,记作②,②-①即可得到前n项和Sn的通项公式;
的前n项和Sn,记作①,两边乘以2得到另一个关系式,记作②,②-①即可得到前n项和Sn的通项公式;


 如图一个同心圆形花坛,分为两部分,中间小圆部分种植草坪和绿色灌木,周围的圆环分为n(n≥3,n∈N)等份,种植红、黄、蓝三色不同的花,要求相邻两部分种植不同颜色的花.如图所示圆环分成的n等份为a1,a2,a3,…,an,有多少不同的种植方法( )
如图一个同心圆形花坛,分为两部分,中间小圆部分种植草坪和绿色灌木,周围的圆环分为n(n≥3,n∈N)等份,种植红、黄、蓝三色不同的花,要求相邻两部分种植不同颜色的花.如图所示圆环分成的n等份为a1,a2,a3,…,an,有多少不同的种植方法( ) 成立的所有N的值.
成立的所有N的值.