Question

【题目】已知命题p：（x+1）（x﹣5）≤0，命题q：1﹣m≤x＜1+m（m＞0）．
（1）若p是q的充分条件，求实数m的取值范围；
（2）若m=5，“p∨q”为真命题，“p∧q”为假命题，求实数x的取值范围．

Answer 1

【答案】
（1）解：由命题p：（x+1）（x﹣5）≤0，化为﹣1≤x≤5．

命题q：1﹣m≤x＜1+m（m＞0）．

∵p是q的充分条件，

∴[﹣1，5][1﹣m，1+m），

∴ ，解得m＞4．

则实数m的取值范围为（4，+∞）

（2）解：∵m=5，∴命题q：﹣4≤x＜6．

∵“p∨q”为真命题，“p∧q”为假命题，

∴命题p，q为一真一假．

当p真q假时，可得 ，解得x∈．

当q真p假时，可得 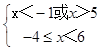，解得﹣4≤x＜﹣1或5＜x＜6．

因此x的取值范围是[﹣4，﹣1）∪（5，6）

【解析】（1）由于p是q的充分条件，可得[﹣1，5][1﹣m，1+m），解出即可；（2）由于“p∨q”为真命题，“p∧q”为假命题，可得命题p，q为一真一假．即可即可．
【考点精析】掌握复合命题的真假是解答本题的根本，需要知道“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反；“p且q”形式复合命题当P与q同为真时为真，其他情况时为假；“p或q”形式复合命题当p与q同为假时为假，其他情况时为真．