
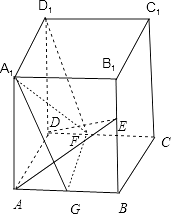
【题目】在正方体ABCD﹣A1B1C1D1中,E、F分别是BB1 , CD的中点,求证:平面ADE⊥平面A1FD1 .
【答案】证明:因为ABCD﹣A1B1C1D1是正方体,
所以AD⊥平面DCC1D1,
又D1F平面DCC1D1,所以AD⊥D1F,
取AB中点G,
连接A1G、FG,因为F为CD中点,
所以FG ![]() AD
AD ![]() A1D1,所以A1G∥D1F,
A1D1,所以A1G∥D1F,
因为E是BB1中点,所以Rt△A1AG≌Rt△ABE,
所以∠AA1G=∠HAG,∠AHA1=90°,
即A1G⊥AE,所以D1F⊥AE,因为AD∩AE=A,
所以D1F⊥平面ADE,
所以D1F平面A1FD1,
所以平面A1FD1⊥平面ADE.
【解析】由已知得AD⊥平面DCC1D1,从而AD⊥D1F,取AB中点G,由已知条件推导出A1G⊥AE,从而D1F⊥AE,进而D1F⊥平面ADE,由此能证明平面A1FD1⊥平面ADE.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦点分别为F1、F2 , 过右焦点F2且与x轴垂直的直线与双曲线两条渐近线分别交于A,B两点,若△ABF1为等腰直角三角形,且|AB|=4
=1(a>0,b>0)的左、右焦点分别为F1、F2 , 过右焦点F2且与x轴垂直的直线与双曲线两条渐近线分别交于A,B两点,若△ABF1为等腰直角三角形,且|AB|=4 ![]() ,P(x,y)在双曲线上,M(
,P(x,y)在双曲线上,M( ![]() ,
, ![]() ),则|PM|+|PF2|的最小值为( )
),则|PM|+|PF2|的最小值为( )
A.![]() ﹣1
﹣1
B.2
C.2 ![]() ﹣2
﹣2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)如下图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E、F分别是BC、CC1的中点.
(1)证明:平面AEF⊥平面B1BCC1;
(2)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F-AEC的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设z1 , z2是复数,则下列命题中的假命题是( )
A.若|z1﹣z2|=0,则 ![]() =
= ![]()
B.若z1= ![]() ,则
,则 ![]() =z2
=z2
C.若|z1|=|z2|,则z1 ![]() =z2
=z2 ![]()
D.若|z1|=|z2|,则z12=z22
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度![]() (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度![]() (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当![]() 不超过4(尾/立方米)时,
不超过4(尾/立方米)时,![]() 的值为
的值为![]() (千克/年);当
(千克/年);当![]() 时,
时,![]() 是
是![]() 的一次函数;当
的一次函数;当![]() 达到
达到![]() (尾/立方米)时,因缺氧等原因,
(尾/立方米)时,因缺氧等原因,![]() 的值为
的值为![]() (千克/年).
(千克/年).
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)当养殖密度![]() 为多大时,鱼的年生长量(单位:千克/立方米)
为多大时,鱼的年生长量(单位:千克/立方米)![]() 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com