
【题目】已知函数f(x)=x3+ax2+bx+a2(a、b∈R)
(1)若函数f(x)在x=1处有极值为10,求b的值;
(2)若a=﹣4,f(x)在x∈[0,2]上单调递增,求b的最小值.
【答案】
(1)解:f'(x)=3x2+2ax+b,
若函数f(x)在x=1处有极值为10,
则 ![]()
![]() 或
或 ![]() ,
,
当 ![]() 时,f'(x)=3x2+8x﹣11,
时,f'(x)=3x2+8x﹣11,
△=64+132>0,所以函数有极值点;
当 ![]() 时,f′(x)=3(x﹣1)2≥0,
时,f′(x)=3(x﹣1)2≥0,
所以函数无极值点;
则b的值为﹣11
(2)解:a=﹣4时,f(x)=x3﹣4x2+bx+16,
f'(x)=3x2﹣8x+b≥0对任意的x∈[0,2]都成立,
即b≥﹣3x2+8x,x∈[0,2],
令h(x)=﹣3x2+8x,对称轴x= ![]() ,
,
函数h(x)在[0, ![]() )递增,在(
)递增,在( ![]() ,2]递减,
,2]递减,
故h(x)max=h( ![]() )=
)= ![]() ,
,
故b≥ ![]() ,
,
则b的最小值为 ![]()
【解析】(1)首先求出![]() ,根据题意得
,根据题意得![]() 且
且![]() ,解关于a,b的方程组
,解关于a,b的方程组![]() 得到
得到![]() 或
或![]() ,经检验当
,经检验当![]() 时函数
时函数![]() 无极值点,舍去。(2)由题意,将原问题转化为
无极值点,舍去。(2)由题意,将原问题转化为![]() ,结合二次函数的性质可得b的最小值为
,结合二次函数的性质可得b的最小值为![]() 。
。
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性和函数的极值与导数的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知△ABC的顶点A(6,1),AB边上的中线CM所在直线方程为2x﹣y﹣7=0,AC边上的高BH所在直线方程为x﹣2y﹣6=0.
(1)求点C的坐标;
(2)求直线BC的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A是抛物线M:y2=2px(p>0)与圆C:x2+(y﹣4)2=a2在第一象限的公共点,且点A到抛物线M焦点F的距离为a,若抛物线M上一动点到其准线与到点C的距离之和的最小值为2a,O为坐标原点,则直线OA被圆C所截得的弦长为( )
A.2
B.2 ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家质量监督检验检疫局于2004年5月31日发布了新的《车辆驾驶人员血液、呼吸酒精含量阀值与检验》国家标准,新标准规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升,小于80毫克/百毫克升为饮酒驾车,血液中的酒精含量大于或等于80毫克/百毫升为醉酒驾车,经过反复试验,喝1瓶啤酒后酒精在人体血液中的变化规律的“散点图”如下:

该函数模型如下:

根据上述条件,回答以下问题:
(1)试计算喝1瓶啤酒后多少小时血液中的酒精含量达到最大值?最大值是多少?
(2)试计算喝1瓶啤酒后多少小时后才可以驾车?(时间以整小时计算)
(参数数据: ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】脱贫是政府关注民生的重要任务,了解居民的实际收入状况就显得尤为重要.现从某地区随机抽取![]() 个农户,考察每个农户的年收入与年积蓄的情况进行分析,设第
个农户,考察每个农户的年收入与年积蓄的情况进行分析,设第![]() 个农户的年收入
个农户的年收入![]() (万元),年积蓄
(万元),年积蓄![]() (万元),经过数据处理得
(万元),经过数据处理得![]()
(Ⅰ)已知家庭的年结余![]() 对年收入
对年收入![]() 具有线性相关关系,求线性回归方程;
具有线性相关关系,求线性回归方程;
(Ⅱ)若该地区的农户年积蓄在![]() 万以上,即称该农户已达小康生活,请预测农户达到小康生活的最低年收入应为多少万元?
万以上,即称该农户已达小康生活,请预测农户达到小康生活的最低年收入应为多少万元?
附:在![]() 中,
中, 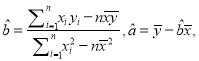 其中
其中![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com