
分析 (1)先求出f(x)的导数,根据f′(0)=0,求出a的值即可;(2)先求出f(x)的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最值.
解答 解:(1)y=f′(x)=$\frac{{e}^{x}}{{e}^{x}+1}$-a,
∴f′(0)=$\frac{{e}^{0}}{{e}^{0}+1}$-a=$\frac{1}{2}$-a=0,
解得:a=$\frac{1}{2}$;
(2)由(1)得:
f(x)=ln(ex+1)-$\frac{1}{2}$x,
∴f′(x)=$\frac{{e}^{x}-1}{2{(e}^{x}+1)}$,
令f′(x)>0,解得:x>0,令f′(x)<0,解得:x<0,
∴f(x)在(-∞,0)递减,在(0,+∞)递增,
∴f(x)最小值=f(0)=ln2,无最大值.
点评 本题考查了求切线的斜率问题,考查函数的单调性、最值问题,考查导数的应用,是一道基础题.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:解答题
 如图所示,某畜牧基地要围成相同面积的羊圈4间,一面可利用原有的墙壁,其余各面用篱笆围成,篱笆总长为36m,则每间羊圈的长和宽各为多少时,羊圈面积最大?
如图所示,某畜牧基地要围成相同面积的羊圈4间,一面可利用原有的墙壁,其余各面用篱笆围成,篱笆总长为36m,则每间羊圈的长和宽各为多少时,羊圈面积最大?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
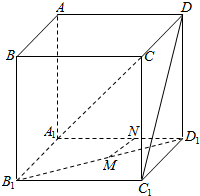 在正方体ABCD-A1B1C1D1中,若M、N分别为B1D1与C1D上的点,且MN⊥B1D,MN⊥C1D1,则MN与A1C的位置关系是MN∥A1C.1.
在正方体ABCD-A1B1C1D1中,若M、N分别为B1D1与C1D上的点,且MN⊥B1D,MN⊥C1D1,则MN与A1C的位置关系是MN∥A1C.1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com