
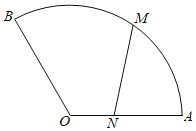
【题目】某公园草坪上有一扇形小径(如图),扇形半径为![]() ,中心角为
,中心角为![]() ,甲由扇形中心
,甲由扇形中心![]() 出发沿
出发沿![]() 以每秒2米的速度向
以每秒2米的速度向![]() 快走,同时乙从
快走,同时乙从![]() 出发,沿扇形弧以每秒
出发,沿扇形弧以每秒![]() 米的速度向
米的速度向![]() 慢跑,记
慢跑,记![]() 秒时甲、乙两人所在位置分别为
秒时甲、乙两人所在位置分别为![]() ,
,![]() ,通过计算
,通过计算![]() ,判断下列说法是否正确:
,判断下列说法是否正确:
(1)当![]() 时,函数
时,函数![]() 取最小值;
取最小值;
(2)函数![]() 在区间
在区间![]() 上是增函数;
上是增函数;
(3)若![]() 最小,则
最小,则![]() ;
;
(4)![]() 在
在![]() 上至少有两个零点;
上至少有两个零点;
其中正确的判断序号是______(把你认为正确的判断序号都填上)
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:
【题目】设集合![]() 由满足下列两个条件的数列
由满足下列两个条件的数列![]() 构成:①
构成:①![]() ②存在实数
②存在实数![]() 使得
使得![]() 对任意正整数
对任意正整数![]() 都成立.
都成立.
(1)现在给出只有5项的有限数列![]() 试判断数列
试判断数列![]() 是否为集合
是否为集合![]() 的元素;
的元素;
(2)设数列![]() 的前项和为
的前项和为![]() 且
且![]() 若对任意正整数
若对任意正整数![]() 点
点![]() 均在直线
均在直线![]() 上,证明:数列
上,证明:数列![]() 并写出实数
并写出实数![]() 的取值范围;
的取值范围;
(3)设数列![]() 若数列
若数列![]() 没有最大值,求证:数列
没有最大值,求证:数列![]() 一定是单调递增数列。
一定是单调递增数列。
查看答案和解析>>
科目:高中数学 来源: 题型:
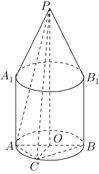
【题目】如图,空间几何体由两部分构成,上部是一个底面半径为1,高为2的圆锥,下部是一个底面半径为1,高为2的圆柱,圆锥和圆柱的轴在同一直线上,圆锥的下底面与圆柱的上底面重合,点![]() 是圆锥的顶点,
是圆锥的顶点,![]() 是圆柱下底面的一条直径,
是圆柱下底面的一条直径,![]() 、
、![]() 是圆柱的两条母线,
是圆柱的两条母线,![]() 是弧
是弧![]() 的中点.
的中点.
(1)求异面直线![]() 与
与![]() 所成的角的大小;
所成的角的大小;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() 、
、![]() 、
、![]() ,如果存在实数
,如果存在实数![]() 、
、![]() 使得
使得![]() ,那么称
,那么称![]() 为
为![]() 、
、![]() 的生成函数.
的生成函数.
(1)若![]() ,
,![]() ,
,![]() ,则
,则![]() 是否分别为
是否分别为![]() 、
、![]() 的生成函数?并说明理由;
的生成函数?并说明理由;
(2)设![]() ,
,![]() ,
,![]() ,
,![]() ,生成函数
,生成函数![]() ,若不等式
,若不等式![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,
,![]() 取
取![]() ,
,![]() ,生成函数
,生成函数![]() 图象的最低点坐标为
图象的最低点坐标为![]() ,若对于任意正实数
,若对于任意正实数![]() 、
、![]() 且
且![]() ,试问是否存在最大的常数
,试问是否存在最大的常数![]() ,使
,使![]() 恒成立?如果存在,求出这个
恒成立?如果存在,求出这个![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图像向左平移
的图像向左平移![]() 个单位长度,再将图像上所有点的横坐标伸长到原来的
个单位长度,再将图像上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变),得到
倍(纵坐标不变),得到![]() 的图像.
的图像.
(1)求![]() 的单调递增区间;
的单调递增区间;
(2)若对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com