练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在三棱锥中，，侧面底面，，为线段上一点，且满足.

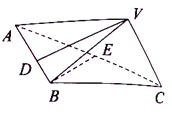
    （1）若为的中点，求证：；

    （2）当最小时，求二面角的余弦值.

    【答案】(1)见证明；(2)

    【解析】

    (1)根据中点可得 ，再根据面面垂直的性质定理得面，即可证明结论(2) 以为坐标原点，分别以射线和垂直于面向上的方向为轴，建立空间直角坐标系，求出两个半平面的法向量，利用公式求其夹角余弦即可.

    （1）在，因为,，

    为的中点，所以，

    因为面面，面面，所以面，

    又面，

    （2）以为坐标原点，分别以射线和垂直于面向上的方向为轴，建立空间直角坐标系，

    设，则有，因为侧面底面，，

    所以，

    所以，

    当时，最小，

    此时，，

    设为平面的一个法向量，则有，

    所以，令，则，

    而平面的一个法向量为，

    所以，

    故二面角的余弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某公司需要对所生产的三种产品进行检测，三种产品数量（单位：件）如下表所示：

    产品

    A

    B

    C

    数量（件）

    180

    270

    90

    采用分层抽样的方法从以上产品中共抽取6件.

    （1）求分别抽取三种产品的件数；

    （2）将抽取的6件产品按种类编号，分别记为，现从这6件产品中随机抽取2件.

    （ⅰ）用所给编号列出所有可能的结果；

    （ⅱ）求这两件产品来自不同种类的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点，，圆C的方程为，过点A的直线l与圆C相切，点P为圆C上的动点.

    （1）求直线l的方程；

    （2）求面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中，正确的共有（ ）

    ① 因为直线是无限的，所以平面内的一条直线就可以延伸到平面外去；

    ② 两个平面有时只相交于一个公共点；

    ③ 分别在两个相交平面内的两条直线如果相交，则交点只可能在两个平面的交线上；

    ④ 一条直线与三角形的两边都相交，则这条直线必在三角形所在的平面内；

    A.0个B.1个C.2个D.3个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】高一(1)班参加校生物竞赛学生的成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如下，据此解答如下问题：

    (1)求高一(1)班参加校生物竞赛的人数及分数在[80,90)之间的频数，并计算频率分布直方图中[80,90)间的矩形的高；

    (2)若要从分数在[80,100]之间的学生中任选2人进行某项研究，求至少有1人分数在[90,100]之间的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某口袋内装有一些除颜色不同之外其他均相同的红球、白球和黑球，从中摸出1个球，摸出红球的概率是0.42，摸出白球的概率是0.28，若红球有21个，则黑球有_________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥PABCD中，底面ABCD是矩形，PA⊥平面ABCD，AD＝1，PA＝AB＝ ，点E是棱PB的中点．

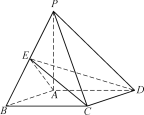
    （1）求异面直线EC与PD所成角的余弦值；

    （2）求二面角B-EC-D的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，侧面是菱形，，是棱的中点，，在线段上，且.

    （1）证明：面；

    （2）若，面面，求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点、，

    （1）若两点到直线的距离都为，求直线的方程；

    （2）若两点到直线的距离都为，试根据的取值讨论直线存在的条数，不需写出直线方程.

    查看答案和解析>>

    同步练习册答案