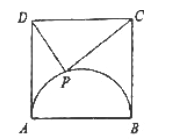
【题目】如图，
是边长为4的正方形，动点
在以
为直径的圆弧
上，则
的取值范围是__________．
【答案】
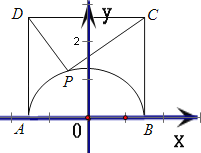
【解析】以AB中点为坐标原点，AB所在直线为x轴建立如图坐标系
则圆弧APB方程为x2+y2=4，（y≥0），C（2，4），D（﹣2，4）
因此设P（2cosα，2sinα），α∈[0，π]
∴
=（2﹣2cosα，4﹣2sinα），
=（﹣2﹣2cosα，4﹣2sinα），
由此可得
=（2﹣2cosα）（﹣2﹣2cosα）+（4﹣2sinα）（4﹣2sinα）
=4cos2α﹣4+16﹣16sinα+4sin2α=16﹣16sinα
化简得=16﹣16sinα
∵α∈[0，π]，sinα∈[0，1]
∴当α=0或π时，取最大值为16；当α=
时，取最小值为0．
由此可得的取值范围是[0，16]
故答案为：[0，16]
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】如图，某城市有一条公路正西方AO通过市中心O后转向北偏东α角方向的OB，位于该市的某大学M与市中心O的距离OM=3 
km，且∠AOM=β，现要修筑一条铁路L，L在OA上设一站A，在OB上设一站B，铁路在AB部分为直线段，且经过大学M，其中tanα=2，cosβ= 
，AO=15km． 
（1）求大学M在站A的距离AM；
（2）求铁路AB段的长AB．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
， 
， 
， 
（1）求证：函数
在点
处的切线恒过定点，并求出定点的坐标；
（2）若
在区间
上恒成立，求
的取值范围；
（3）当
时，求证：在区间
上，满足
恒成立的函数
有无穷多个．（记
）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设f（x）是定义在R上的函数，对任意实数m，n，都有f（m）f（n）=f（m+n），且当x＜0时，0＜f（x）＜1．
（1）证明：①f（0）=1；②当x＞0时，f（x）＞1；③f（x）是R上的增函数；
（2）设a∈R，试解关于x的不等式f（x2﹣3ax+1）f（﹣3x+6a+1）≤1．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=（2﹣a）（x﹣1）﹣2lnx，g（x）= 
（a∈R，e为自然对数的底数）
（Ⅰ）当a=1时，求f（x）的单调区间；
（Ⅱ）若函数f（x）在
上无零点，求a的最小值；
（Ⅲ）若对任意给定的x0∈（0，e]，在（0，e]上总存在两个不同的xi（i=1，2），使得f（xi）=g（x0）成立，求a的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
