
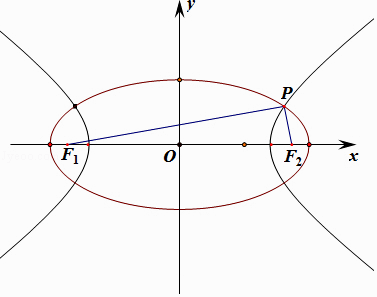
【题目】已知椭圆C1与双曲线C2有相同的左右焦点F1、F2 , P为椭圆C1与双曲线C2在第一象限内的一个公共点,设椭圆C1与双曲线C2的离心率为e1 , e2 , 且 ![]() =
= ![]() ,若∠F1PF2=
,若∠F1PF2= ![]() ,则双曲线C2的渐近线方程为( )
,则双曲线C2的渐近线方程为( )
A.x±y=0
B.x± ![]() y=0
y=0
C.x± ![]() y=0
y=0
D.x±2y=0
【答案】C
【解析】解:设椭圆C1的方程: ![]() (a1>b1>0),双曲线C2的方程:
(a1>b1>0),双曲线C2的方程: ![]() (a2>0,b2>0),
(a2>0,b2>0),
焦点F1(﹣c,0),F2(c,0),
由e1= ![]() ,e1=
,e1= ![]() ,由
,由 ![]() =
= ![]() ,则
,则 ![]() =
= ![]() ,则a1=3a2,
,则a1=3a2,
由题意的定义:丨PF1丨+丨PF2丨=2a1,丨PF1丨﹣丨PF2丨=2a2,
则丨PF1丨=a1+a2=4a2,丨PF2丨=a1﹣a2=2a2,
由余弦定理可知:丨F1F2丨2=丨PF1丨2+丨PF1丨2﹣2丨PF1丨丨PF1丨cos∠F1PF2,
则(2c)2=(4a2)2+(2a2)2﹣2×4a2×2a2× ![]() ,
,
c2=3a22,b22=c2﹣a22=2a22,则b2= ![]() a2,
a2,
双曲线的渐近线方程y=± ![]() x=±
x=± ![]() x,即x±
x,即x± ![]() y=0,
y=0,
故选:C.


科目:高中数学 来源: 题型:
【题目】某种产品的广告费用支出![]() 与销售额
与销售额![]() 之间有如下的对应数据(单位:万元):
之间有如下的对应数据(单位:万元):
![]()
(1)求![]() 关于
关于![]() 的线性回归直线方程;
的线性回归直线方程;
(2)据此估计广告费用为10万元时销售收入![]() 的值.
的值.
(附:对于线性回归方程![]() ,其中
,其中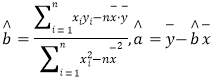 )
)
参考公式: 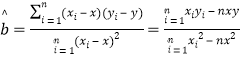
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=a(x﹣lnx)+ ![]() ,a∈R.
,a∈R.
(I)讨论f(x)的单调性;
(II)当a=1时,证明f(x)>f′(x)+ ![]() 对于任意的x∈[1,2]成立.
对于任意的x∈[1,2]成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的首项a1=2,前n项和为Sn , 等比数列{bn}的首项b1=1,且a2=b3 , S3=6b2 , n∈N* .
(1)求数列{an}和{bn}的通项公式;
(2)数列{cn}满足cn=bn+(﹣1)nan , 记数列{cn}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知角x始边与x轴的非负半轴重合,与圆x2+y2=4相交于点A,终边与圆x2+y2=4相交于点B,点B在x轴上的射影为C,△ABC的面积为S(x),函数y=S(x)的图象大致是( )
A.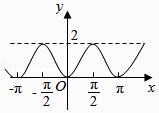
B.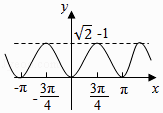
C.
D.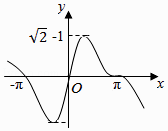
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题: ①x∈(0,2),3x>x3的否定是:x∈(0,2),3x≤x3;
②若f(x)=2x﹣2﹣x , 则x∈R,f(﹣x)=﹣f(x);
③若f(x)=x+ ![]() ,x0∈(0,+∞),f(x0)=1;
,x0∈(0,+∞),f(x0)=1;
④在△ABC中,若A>B,则sin A>sin B.
其中真命题是 . (将所有真命题序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (t为参数,a>0).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4cosθ.
(t为参数,a>0).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4cosθ.
(Ⅰ)说明C1是哪一种曲线,并将C1的方程化为极坐标方程;
(Ⅱ)直线C3的极坐标方程为θ=α0 , 其中α0满足tanα0=2,若曲线C1与C2的公共点都在C3上,求a.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com