
分析 (1)对数要求真数大于0,从而便可得出该函数定义域为(2,+∞),并且容易看出f(3)=0,这样所过的定点也找到了;
(2)根据对数函数的单调性,讨论a:a>1,和0<a<1,根据每种情况下f(x)的单调性,求出f(x)的最大值,这样即可建立关于a的方程,解方程得出a的值,并判断是否满足a假设的范围.
解答 解:(1)要使函数f(x)有意义,则x-2>0;
∴x>2;
∴该函数的定义域为(2,+∞);
f(3)=0;
∴f(x)的图象过定点(3,0);
(2)①若a>1,则f(x)在[4,6]上为增函数;
∴最大值为f(6)=loga4=2;
∴a2=4;
∴a=2;
②若0<a<1,则f(x)为减函数;
∴f(x)在[4,6]上的最大值为f(4)=loga2=2;
∴a2=2;
∴$a=\sqrt{2}$>1;
∴这种情况不存在;
∴实数a的值为2.
点评 考查函数定义域的概念,对数函数的定义域的求法,函数图象所过定点的求法,以及对数函数的单调性,根据单调性定义求函数的最大值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
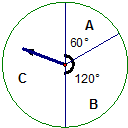 五一节期间,某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置,指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见右上表.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
五一节期间,某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置,指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见右上表.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.| 指针位置 | A区域 | B区域 | C区域 |
| 返券金额(单位:元) | 60 | 30 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分有不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com