
【题目】在正四面体![]() 中,
中,![]() 分别是
分别是![]() 的中点,下面四个结论:
的中点,下面四个结论:![]()
①![]() //平面
//平面![]()
②![]() 平面
平面![]()
③平面![]() 平面
平面![]()
④平面![]() 平面
平面![]()
![]()
其中正确结论的序号是______________.
【答案】①②④
【解析】
如图所示,由已知条件利用线面平行,线面垂直,面面垂直的判定直接推导即可得出答案.

如图所示,在正四面体P-ABC中,D,F分别是AB,CA的中点,则DF//BC,
因为![]() 平面PDF,BC平面PDF,所以BC//平面PDF,故①正确;
平面PDF,BC平面PDF,所以BC//平面PDF,故①正确;
由PB=PC,AB=AC,E为中点,得![]() ,所以
,所以![]() 平面PAE,由DF//BC得DF
平面PAE,由DF//BC得DF![]() 平面PAE,故②正确;
平面PAE,故②正确;
过P作PO![]() 平面ABC,垂足为O,由题意得O点为底面△ABC的中心,且点O在AE上,AO=
平面ABC,垂足为O,由题意得O点为底面△ABC的中心,且点O在AE上,AO=![]() AE,
AE,
设AE与DF的交点为M,则由AM=![]() AE,故点O,M不重合,则平面PDF和平面ABC不垂直,故③不正确;
AE,故点O,M不重合,则平面PDF和平面ABC不垂直,故③不正确;
由②得![]() 平面PAE,BC平面PBC,所以平面PBC
平面PAE,BC平面PBC,所以平面PBC![]() 平面PAE,故④正确,综上可得正确的序号为①②④.
平面PAE,故④正确,综上可得正确的序号为①②④.
故答案为:①②④.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:
【题目】某赛季甲、乙两名篮球运动员各13场比赛得分情况用茎叶图表示如图:
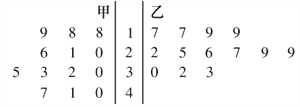
根据上图,对这两名运动员地成绩进行比较,下列四个结论中,不正确的是
A. 甲运动员得分的极差大于乙运动员得分的极差
B. 甲运动员得分的中位数大于乙运动员得分的中位数
C. 甲运动员的得分平均值大于乙运动员的得分平均值
D. 甲运动员的成绩比乙运动员的成绩稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,线段
上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 作不与
作不与![]() 轴重合的直线
轴重合的直线![]() ,设
,设![]() 与圆
与圆![]() 相交于
相交于![]() 两点,与椭圆相交于
两点,与椭圆相交于![]() 两点,当
两点,当![]() 且
且![]() 时,求
时,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.若a,b是两条直线,且a∥b,那么a平行于经过b的任何平面
B.若直线a和平面α满足a∥α,那么a与α内的任何直线平行
C.平行于同一条直线的两个平面平行
D.若直线a,b和平面α满足a∥b,a∥α,b不在平面α内,则b∥α
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的中点.

(1)求证:MN∥平面PAD;
(2)在PB上确定一个点Q,使平面MNQ∥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位从一所学校招收某类特殊人才,对![]() 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:

例如,表中运动协调能力良好且逻辑思维能力一般的学生有![]() 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这![]() 位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)从参加测试的![]() 位学生中任意抽取
位学生中任意抽取![]() 位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
(III)从参加测试的![]() 位学生中任意抽取
位学生中任意抽取![]() 位,设运动协调能力或逻辑思维能力优秀的学生人数为
位,设运动协调能力或逻辑思维能力优秀的学生人数为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com