
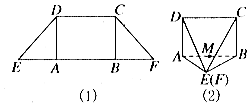 如图所示,在等腰梯形CDEF中,DE=CD=$\sqrt{2}$,EF=2+$\sqrt{2}$,将它沿着两条高AD,CB折叠成如图(2)所示的四棱锥E-ABCD(E,F重合).
如图所示,在等腰梯形CDEF中,DE=CD=$\sqrt{2}$,EF=2+$\sqrt{2}$,将它沿着两条高AD,CB折叠成如图(2)所示的四棱锥E-ABCD(E,F重合).分析 (1)证明AD⊥平面ABE,AD⊥BE,AE⊥BE,再用一次线面垂直的判定定理得到BE⊥面DAE,所以DE⊥BE;
(2)取EC的中点G,BE的中点P,连接PM,PG,MG.利用三角形中位线定理结合线面平行的判定,得到MP∥平面DAE,GP∥平面DAE,从而平面MPG∥平面DAE,由此得到直线MG∥平面DAE,可得点N就是点G.
解答  (1)证明:∵AD⊥EF,∴AD⊥AE,AD⊥AB.
(1)证明:∵AD⊥EF,∴AD⊥AE,AD⊥AB.
又∵AB∩AE=A,
∴AD⊥平面ABE,∴AD⊥BE.
由题图(1)和题中所给条件知,四棱锥E-ABCD中,AE=BE=1,AB=CD=$\sqrt{2}$,
∴AE2+BE2=AB2,即AE⊥BE.
又∵AE∩AD=A,
∴BE⊥平面ADE,∴BE⊥DE…(6分)
(2)解:取EC的中点G,BE的中点P,连接PM,PG,MG,
则MP∥AE,GP∥CB∥DA,
∴MP∥平面DAE,GP∥平面DAE.
∵MP∩GP=P,∴平面MPG∥平面DAE.
∵MG?平面MPG,∴MG∥平面DAE,
故当点N与点G重合时满足条件…(12分)
点评 本题证明了线线垂直和线面平行,着重考查了空间平行与垂直位置关系的证明等知识,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | x=-1 | B. | y=-1 | C. | x=-2 | D. | y=-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “若a>1,则a2>1”的否命题是“若a>1,则a2≤1” | |
| B. | 在△ABC中,“A>B”是“sin2A>sin2B”必要不充分条件 | |
| C. | “若tanα$≠\sqrt{3}$,则$α≠\frac{π}{3}$”是真命题 | |
| D. | ?x0∈(-∞,0)使得3${\;}^{{x}_{0}}$<4${\;}^{{x}_{0}}$成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{2}$ | B. | 向左平移$\frac{π}{2}$ | C. | 向左平移$\frac{π}{4}$ | D. | 向右平移$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com