
【题目】已知函数y= 4cos2x+4![]() sinxcosx-2,(x∈R)
sinxcosx-2,(x∈R)
(1)求函数的最小正周期;
(2)求函数的最大值及其相对应的x值;
(3)写出函数的单调增区间;
(4)写出函数的对称轴
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,侧棱
,侧棱![]() ,底面
,底面![]() 是直角梯形,其中
是直角梯形,其中![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() .
.
(2)试问在棱![]() 上是否存在点
上是否存在点![]() ,使得面
,使得面![]() 面
面![]() ,若存在,试指出点
,若存在,试指出点![]() 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.

(1)求频率分布直方图中a的值;
(2)估计总体中成绩落在[50,60)中的学生人数;
(3)根据频率分布直方图估计20名学生数学考试成绩的众数,平均数;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有6个球,其中4个白球,2个红球,从袋中任意取出两球,求下列事件的概率:
(1) 取出的两球1个是白球,另1个是红球;
(2) 取出的两球至少一个是白球。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,MN分别是边长为1的正方形ABCD的边BCCD的中点,将正方形沿对角线AC折起,使点D不在平面ABC内,则在翻折过程中,有以下结论:

①异面直线AC与BD所成的角为定值.
②存在某个位置,使得直线AD与直线BC垂直.
③存在某个位置,使得直线MN与平面ABC所成的角为45°.
④三棱锥M-ACN体积的最大值为![]() .
.
以上所有正确结论的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,上顶点为
,上顶点为![]() ,若直线
,若直线![]() 的斜率为1,且与椭圆的另一个交点为
的斜率为1,且与椭圆的另一个交点为![]() ,
, ![]() 的周长为
的周长为![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 的直线
的直线![]() (直线
(直线![]() 的斜率不为1)与椭圆交于
的斜率不为1)与椭圆交于![]() 两点,点
两点,点![]() 在点
在点![]() 的上方,若
的上方,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C:![]() 的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为
的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为![]() ,|F1F2|=
,|F1F2|=![]() ,O为坐标原点.
,O为坐标原点.
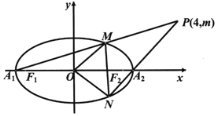
(1)求椭圆C的方程;
(2)设过点P(4,m)的直线PA1,PA2与椭圆分别交于点M,N,其中m>0,求![]() 的面积S的最大值.
的面积S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com