
【题目】受轿车在保修期内维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年.现从该厂已售出的两种品牌轿车中各随机抽取50辆,统计数据如下:
品牌 | 甲 | 乙 | |||
首次出现故 障时间x(年) | 0<x≤1 | 1<x≤2 | x>2 | 0<x≤2 | x>2 |
轿车数量(辆) | 2 | 3 | 45 | 5 | 45 |
每辆利润 (万元) | 1 | 2 | 3 | 1.8 | 2.9 |
将频率视为概率,解答下列问题:
(1)从该厂生产的甲品牌轿车中随机抽取一辆,求其首次出现故障发生在保修期内的概率.
(2)若该厂生产的轿车均能售出,记生产一辆甲品牌轿车的利润为X1,生产一辆乙品牌轿车的利润为X2,分别求X1,X2的分布列.
(3)该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌的轿车.若从经济效益的角度考虑,你认为应生产哪种品牌的轿车?说明理由.
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
, ![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 上一动点(异于点
上一动点(异于点![]() ),
),![]() 为线段
为线段![]() 上一动点,且
上一动点,且![]() .
.
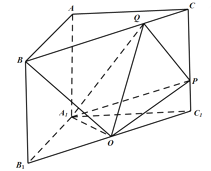
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】省环保厅对![]() 、
、![]() 、
、![]() 三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
|
|
| |
优(个) | 28 |
|
|
良(个) | 32 | 30 |
|
已知在这180个数据中随机抽取一个,恰好抽到记录![]() 城市空气质量为优的数据的概率为0.2.
城市空气质量为优的数据的概率为0.2.
(1)现按城市用分层抽样的方法,从上述180个数据中抽取30个进行后续分析,求在![]() 城中应抽取的数据的个数;
城中应抽取的数据的个数;
(2)已知![]() ,
, ![]() ,求在
,求在![]() 城中空气质量为优的天数大于空气质量为良的天数的概率.
城中空气质量为优的天数大于空气质量为良的天数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部门在同一上班高峰时段对甲、乙两座地铁站各随机抽取了50名乘客,统计其乘车等待时间(指乘客从进站口到乘上车的时间,乘车等待时间不超过40分钟).将统计数据按![]() ,
,![]() ,
,![]() ,
,![]() 分组,制成频率分布直方图:
分组,制成频率分布直方图:

(1)求![]() 的值;
的值;
(2)记![]() 表示事件“在上班高峰时段某乘客在甲站乘车等待时间少于20分钟”,试估计
表示事件“在上班高峰时段某乘客在甲站乘车等待时间少于20分钟”,试估计![]() 的概率;
的概率;
(3)假设同组中的每个数据用该组区间左端点值来估计,记在上班高峰时段甲、乙两站各抽取的50名乘客乘车的平均等待时间分别为![]() ,
,![]() ,求
,求![]() 的值,并直接写出
的值,并直接写出![]() 与
与![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)若函数![]() 在区间
在区间![]() 上是单调函数,试求实数
上是单调函数,试求实数![]() 的取值范围;
的取值范围;
(2)已知函数![]() ,且
,且![]() ,若函数
,若函数![]() 在区间
在区间![]() 上恰有3个零点,求实数
上恰有3个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】浦东一模之后的“大将” 洗心革面,再也没进过网吧,开始发奋学习. 2019年春节档非常热门的电影《流浪地球》引发了他的思考:假定地球(设为质点![]() ,地球半径忽略不计)借助原子发动机开始流浪的轨道是以木星(看作球体,其半径约为
,地球半径忽略不计)借助原子发动机开始流浪的轨道是以木星(看作球体,其半径约为![]() 万米)的中心
万米)的中心![]() 为右焦点的椭圆
为右焦点的椭圆![]() . 已知地球的近木星点
. 已知地球的近木星点![]() (轨道上离木星表面最近的点)到木星表面的距离为
(轨道上离木星表面最近的点)到木星表面的距离为![]() 万米,远木星点
万米,远木星点![]() (轨道上离木星表面最远的点)到木星表面的距离为
(轨道上离木星表面最远的点)到木星表面的距离为![]() 万米.
万米.

(1)求如图给定的坐标系下椭圆![]() 的标准方程;
的标准方程;
(2)若地球在流浪的过程中,由![]() 第一次逆时针流浪到与轨道中心
第一次逆时针流浪到与轨道中心![]() 的距离为
的距离为![]() 万米时(其中
万米时(其中![]() 分别为椭圆的长半轴、短半轴的长),由于木星引力,部分原子发动机突然失去了动力,此时地球向着木星方向开始变轨(如图所示),假定地球变轨后的轨道为一条直线
分别为椭圆的长半轴、短半轴的长),由于木星引力,部分原子发动机突然失去了动力,此时地球向着木星方向开始变轨(如图所示),假定地球变轨后的轨道为一条直线![]() ,称该直线的斜率
,称该直线的斜率![]() 为“变轨系数”. 求“变轨系数”
为“变轨系数”. 求“变轨系数”![]() 的取值范围,使地球与木星不会发生碰撞. (精确到小数点后一位)
的取值范围,使地球与木星不会发生碰撞. (精确到小数点后一位)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com