
【题目】下列说法正确的是( )
A.设m为实数,若方程![]() 表示双曲线,则m>2.
表示双曲线,则m>2.
B.“p∧q为真命题”是“p∨q为真命题”的充分不必要条件
C.命题“x∈R,使得x2+2x+3<0”的否定是:“x∈R,x2+2x+3>0”
D.命题“若x0为y=f(x)的极值点,则f’(x)=0”的逆命题是真命题
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且与双曲线
,且与双曲线![]() 有相同的焦点.
有相同的焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,点
两点,点![]() 满足
满足![]() ,点
,点![]() ,若直线
,若直线![]() 斜率为
斜率为![]() ,求
,求![]() 面积的最大值及此时直线
面积的最大值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]()
![]() 过点
过点![]() 两个焦点为
两个焦点为![]() 和
和![]() .圆O的方程为
.圆O的方程为![]() .
.
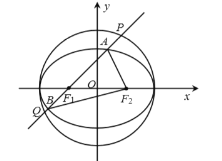
(1)求椭圆C的标准方程;
(2)过![]() 且斜率为
且斜率为![]() 的动直线l与椭圆C交于A、B两点,与圆O交于P、Q两点(点A、P在x轴上方),当
的动直线l与椭圆C交于A、B两点,与圆O交于P、Q两点(点A、P在x轴上方),当![]()
![]()
![]() 成等差数列时,求弦PQ的长.
成等差数列时,求弦PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大数据时代对于现代人的数据分析能力要求越来越高,数据拟合是一种把现有数据通过数学方法来代入某条数式的表示方式,比如![]() ,
,![]()
![]() ,2,
,2,![]() ,n是平面直角坐标系上的一系列点,用函数
,n是平面直角坐标系上的一系列点,用函数![]() 来拟合该组数据,尽可能使得函数图象与点列
来拟合该组数据,尽可能使得函数图象与点列![]() 比较接近.其中一种描述接近程度的指标是函数的拟合误差,拟合误差越小越好,定义函数
比较接近.其中一种描述接近程度的指标是函数的拟合误差,拟合误差越小越好,定义函数![]() 的拟合误差为:
的拟合误差为:![]() .已知平面直角坐标系上5个点的坐标数据如表:
.已知平面直角坐标系上5个点的坐标数据如表:
x | 1 | 3 | 5 | 7 | 9 |
y | 12 |
| 4 |
| 12 |
![]() 若用一次函数
若用一次函数![]() 来拟合上述表格中的数据,求该函数的拟合误差
来拟合上述表格中的数据,求该函数的拟合误差![]() 的最小值,并求出此时的函数解析式
的最小值,并求出此时的函数解析式![]() ;
;
![]() 若用二次函数
若用二次函数![]() 来拟合题干表格中的数据,求
来拟合题干表格中的数据,求![]() ;
;
![]() 请比较第
请比较第![]() 问中的
问中的![]() 和第
和第![]() 问中的
问中的![]() ,用哪一个函数拟合题目中给出的数据更好?
,用哪一个函数拟合题目中给出的数据更好?![]() 请至少写出三条理由
请至少写出三条理由![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,等比数列
,等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]()
(1)设![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)在(1)的条件下,且![]() ,求满足
,求满足![]() 的所有正整数
的所有正整数![]() ;
;
(3)若存在正整数![]() ,且
,且![]() ,试比较
,试比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为![]() ,(t为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C1:ρ=2cosθ,
,(t为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C1:ρ=2cosθ,![]() .
.
(1)求C1与C2交点的直角坐标;
(2)若直线l与曲线C1,C2分别相交于异于原点的点M,N,求|MN|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,AC与BD交于点O,PO⊥平面ABCD,E为CD的中点连接AE交BD于G,点F在侧棱PD上,且DF![]() PD.
PD.
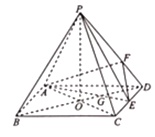
(1)求证:PB∥平面AEF;
(2)若![]() ,求三棱锥E﹣PAD的体积.
,求三棱锥E﹣PAD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,
, ![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
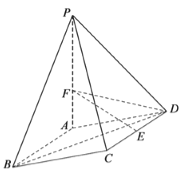
(1)求证:![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)判断直线![]() 与平面
与平面![]() 的位置关系,请说明理由.
的位置关系,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() . 对于函数
. 对于函数![]() 、
、![]() ,若存在常数
,若存在常数![]() ,
,![]() ,使得
,使得![]() ,不等式
,不等式![]() 都成立,则称直线是
都成立,则称直线是![]() 函数
函数![]() 与
与![]() 的分界线.
的分界线.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,试探究函数
时,试探究函数![]() 与
与![]() 是否存在“分界线”?若存在,求出分界线方程;若不存在说明理由.
是否存在“分界线”?若存在,求出分界线方程;若不存在说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com