
科目:高中数学 来源: 题型:选择题
| A. | enf(-n)<f(0),f(n)>enf(0) | B. | enf(-n)<f(0),f(n)<enf(0) | ||
| C. | enf(-n)>f(0),f(n)>enf(0) | D. | enf(-n)>f(0),f(n)<enf(0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥2+$\sqrt{3}$ | B. | 0<a<2-$\sqrt{3}$ | C. | a≥2+$\sqrt{3}$或0<a<1 | D. | a≥2+$\sqrt{3}$或0<a<2-$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
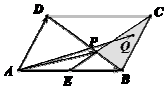 如图,在平行四边形ABCD中,点E为边AB的中点,BD与CE交于点P,若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{AD}(x,y∈R)$,则2x+y=;若点Q是△BCP内部(包括边界)一动点,且$\overrightarrow{AQ}=m\overrightarrow{AB}+n\overrightarrow{AD}(m,n∈R)$,则m+2n的取值范围为[1,3].
如图,在平行四边形ABCD中,点E为边AB的中点,BD与CE交于点P,若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{AD}(x,y∈R)$,则2x+y=;若点Q是△BCP内部(包括边界)一动点,且$\overrightarrow{AQ}=m\overrightarrow{AB}+n\overrightarrow{AD}(m,n∈R)$,则m+2n的取值范围为[1,3].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
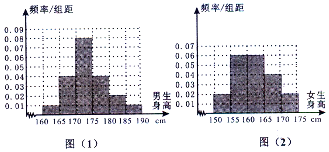 某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1)和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有16人.
某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1)和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有16人.| ≥170cm | <170cm | 总计 | |
| 男生身高 | 30 | 10 | 40 |
| 女生身高 | 4 | 36 | 40 |
| 总计 | 34 | 46 | 80 |
| p(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.445 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com