
分析 (1)利用奇函数的定义,求f(1)的值;
(2)利用函数单调性的定义,得出具体不等式,即可求实数a的取值范围.
解答 解:(1)因为函数y=f(x)(x≠0)是奇函数,∴f(-1)=-f(1)=0即f(1)=0;
(2)∵当x∈(0,+∞)时f(x)是增函数,
∴$f(a-\frac{1}{2})<0$可化为$\left\{{\begin{array}{l}{a-\frac{1}{2}>0}\\{f(a-\frac{1}{2})<f(1)}\end{array}}\right.$或$\left\{{\begin{array}{l}{a-\frac{1}{2}<0}\\{f(a-\frac{1}{2})<f(-1)}\end{array}}\right.$,
即$0<a-\frac{1}{2}<1$或$a-\frac{1}{2}<-1$,
解得$\frac{1}{2}<a<\frac{3}{2}$或$a<-\frac{1}{2}$.
点评 本题考查奇函数的定义,考查函数单调性的运用,考查学生分析解决问题的能力,属于中档题.


 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源:2015-2016学年江西省南昌市高二文下学期期末考试数学试卷(解析版) 题型:选择题
已知定义在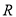 上的函数
上的函数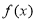 为单调函数,且对任意
为单调函数,且对任意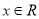 ,恒有
,恒有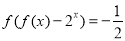 ,若
,若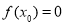 ,则
,则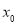 的值是( )
的值是( )
A.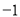 B.
B.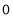 C.
C.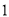 D.
D.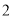
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M,N,P三点共线 | B. | M,N,Q三点共线 | C. | M,P,Q三点共线 | D. | N,P,Q三点共线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 用水量(吨) | [0,10] | (10,20] | (20,30] | (30,40] | (40,50] | 合计 |
| 频数 | 200 | 400 | 200 | b | 100 | 1000 |
| 频率 | 0.2 | a | 0.2 | 0.1 | c | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(5)<f(2)<f(-1) | B. | f(2)<f(5)<f(-1) | C. | f(-1)<f(2)<f(5) | D. | f(2)<f(-1)<f(5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-2\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | -4 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com