
【题目】如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D(不为原点).
(Ⅰ)求点D的轨迹方程;
(Ⅱ)若点D坐标为(2,1),求p的值.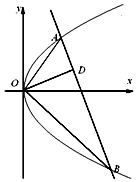
【答案】解:(Ⅰ)设点A的坐标(x1 , y1),点B的坐标(x2 , y2),点D的坐标为(x0 , y0)(x0≠0), 由OA⊥OB得x1x2+y1y2=0.
由已知,得直线AB的方程为 ![]() .
.
又有 ![]() ,
,
由x1x2+y1y2=0得 ![]() .
.
把 ![]() 代入y2=2px并消去x得
代入y2=2px并消去x得 ![]() ,
,
得 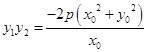
代入 ![]()
得 ![]()
故所求点D的轨迹方程为x2+y2﹣2px=0(x≠0).
(Ⅱ)把x=2,y=1代入方程x2+y2﹣2px=0中,得 ![]()
【解析】(Ⅰ)设点A的坐标(x1 , y1),点B的坐标(x2 , y2),点D的坐标为(x0 , y0)(x0≠0),由OA⊥OB,得x1x2+y1y2=0,由此入手能求出点D的方程.(Ⅱ)点D(2,1)代入方程x2+y2﹣2px=0,能求出结果.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在四边形ABCD中,已知 ![]() ∥
∥ ![]() ,
, ![]() =(6,1),
=(6,1), ![]() =(x,y),
=(x,y), ![]() =(﹣2,﹣3).
=(﹣2,﹣3).
(1)求用x表示y的关系式;
(2)若 ![]() ⊥
⊥ ![]() ,求x、y值.
,求x、y值.
查看答案和解析>>
科目:高中数学 来源: 题型:
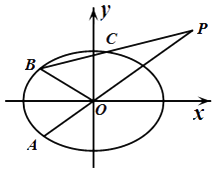
【题目】如图,在平面直角坐标系xOy中,已知椭圆 ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() .A为椭圆上异于顶点的一点,点P满足
.A为椭圆上异于顶点的一点,点P满足 ![]() =
= ![]() ,
, 
(1)若点P的坐标为(2, ![]() ),求椭圆的方程;
),求椭圆的方程;
(2)设过点P的一条直线交椭圆于B,C两点,且 ![]() =m
=m ![]() ,直线OA,OB的斜率之积﹣
,直线OA,OB的斜率之积﹣ ![]() ,求实数m的值;
,求实数m的值;
(3)在(1)的条件下,是否存在定圆M,使得过圆M上任意一点T都能作出该椭圆的两条切线,且这两条切线互相垂直?若存在,求出定圆M;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的三个顶点分别为A(1,0),B(1,4),C(3,2),直线l经过点D(0,4).
(1)判断△ABC的形状;
(2)求△ABC外接圆M的方程;
(3)若直线l与圆M相交于P,Q两点,且PQ=2 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
设函数f(x)=x2-x+15,且|x-a|<1,
(1)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)求证:|f(x)-f(a)|<2(|a|+1).
查看答案和解析>>
科目:高中数学 来源: 题型:
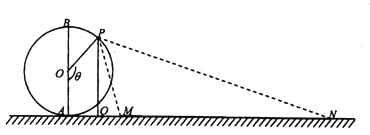
【题目】如图,摩天轮的半径![]() 为
为![]() ,它的最低点
,它的最低点![]() 距地面的高度忽略不计.地上有一长度为
距地面的高度忽略不计.地上有一长度为![]() 的景观带
的景观带![]() ,它与摩天轮在同一竖直平面内,且
,它与摩天轮在同一竖直平面内,且![]() .点
.点![]() 从最低点
从最低点![]() 处逆时针方向转动到最高点
处逆时针方向转动到最高点![]() 处,记
处,记![]() .
.
(1)当![]() 时,求点
时,求点![]() 距地面的高度
距地面的高度![]() ;
;
(2)试确定![]() 的值,使得
的值,使得![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,经过B(1,2)作两条互相垂直的直线l1和l2 , l1交y轴正半轴于点A,l2交x轴正半轴于点C. 
(1)若A(0,1),求点C的坐标;
(2)试问是否总存在经过O,A,B,C四点的圆?若存在,求出半径最小的圆的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com