
【题目】如图,点![]() 在以
在以![]() 为直径的圆
为直径的圆![]() 上,
上,![]() 垂直与圆
垂直与圆![]() 所在平面,
所在平面,![]() 为
为![]() 的垂心.
的垂心.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)延长![]() 交
交![]() 于点
于点![]() ,由重心性质及中位线性质可得
,由重心性质及中位线性质可得![]() ,再结合圆的性质得
,再结合圆的性质得![]() ,由已知
,由已知![]() ,可证
,可证![]() 平面
平面![]() ,进一步可得平面
,进一步可得平面![]() 平面
平面![]() (2)以点
(2)以点![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 方向分别为
方向分别为![]() ,
, ![]() ,
, ![]() 轴正方向建立空间直角坐标系,写出各点坐标,利用二面角与二个半平面的法向量的夹角间的关系可求二面角的余弦值.
轴正方向建立空间直角坐标系,写出各点坐标,利用二面角与二个半平面的法向量的夹角间的关系可求二面角的余弦值.
试题解析:(1)如图,延长![]() 交
交![]() 于点
于点![]() .因为
.因为![]() 为
为![]() 的重心,所以
的重心,所以![]() 为
为![]() 的中点.
的中点.
因为![]() 为
为![]() 的中点,所以
的中点,所以![]() .因为
.因为![]() 是圆
是圆![]() 的直径,所以
的直径,所以![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() .又
.又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() =
= ![]() ,所以
,所以![]() 平面
平面![]() .即
.即![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以平面
,所以平面![]()
![]() 平面
平面![]() .
.

(2)以点![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 方向分别为
方向分别为![]() ,
, ![]() ,
, ![]() 轴正方向建立空间直角坐标系
轴正方向建立空间直角坐标系![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
,  ,
, ![]() ,
, ![]() ,则
,则 ,
,  .平面
.平面![]() 即为平面
即为平面![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则 令
令![]() ,得
,得![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,由
,由![]() 平面
平面![]() ,易得
,易得![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,即
,即![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
在![]() 中,由
中,由![]() ,得
,得![]() ,则
,则![]() ,
, ![]() .
.
所以![]() ,
, ![]() .所以
.所以 .
.
设二面角![]() 的大小为
的大小为![]() ,则
,则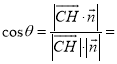
 .
.


科目:高中数学 来源: 题型:
【题目】四面体ABCD中,AB和CD为对棱.设AB=a,CD=b,且异面直线AB与CD间的距离为d,夹角为θ.
(Ⅰ)若θ= ![]() ,且棱AB垂直于平面BCD,求四面体ABCD的体积;
,且棱AB垂直于平面BCD,求四面体ABCD的体积;
(Ⅱ)当θ= ![]() 时,证明:四面体ABCD的体积为一定值;
时,证明:四面体ABCD的体积为一定值;
(Ⅲ)求四面体ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个路口的红绿灯,红灯亮的时间为40秒,黄灯亮的时间为5秒,绿灯亮的时间为50秒(没有两灯同时亮),当你到达路口时,看见下列三种情况的概率各是多少?
(1)红灯;
(2)黄灯;
(3)不是红灯.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知D是以点A(4,1),B(﹣1,﹣6),C(﹣2,3)为顶点的三角形区域(包括边界及内部).
(1)写出表示区域D的不等式组;
(2)设点B(﹣1,﹣6)、C(﹣2,3)在直线4x﹣3y﹣a=0的异侧,求a的取值范围;
(3)若目标函数z=kx+y(k<0)的最小值为﹣k﹣6,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】20名同学参加某次数学考试成绩(单位:分)的频率分布直方图如下:

(Ⅰ)求频率分布直方图中![]() 的值;
的值;
(Ⅱ)分别求出成绩落在![]() ,
, ![]() 中的学生人数;
中的学生人数;
(Ⅲ)从成绩在![]() 的学生中任选2人,求此2人的成绩都在
的学生中任选2人,求此2人的成绩都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 过点
过点![]() ,
, ![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的右、下顶点,且
的右、下顶点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 在椭圆
在椭圆![]() 内,满足直线
内,满足直线![]() ,
, ![]() 的斜率乘积为
的斜率乘积为![]() ,且直线
,且直线![]() ,
, ![]() 分别交椭圆
分别交椭圆![]() 于点
于点![]() ,
, ![]() .
.
(i) 若![]() ,
, ![]() 关于
关于![]() 轴对称,求直线
轴对称,求直线![]() 的斜率;
的斜率;
(ii) 求证: ![]() 的面积与
的面积与![]() 的面积相等.
的面积相等.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com