
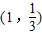 是函数f(x)=ax(a>0且a≠1)的图象上一点,等比数列an的前n项和为f(n)-c,数列bn(bn>0)的首项为c,且前n项和Sn满足:
是函数f(x)=ax(a>0且a≠1)的图象上一点,等比数列an的前n项和为f(n)-c,数列bn(bn>0)的首项为c,且前n项和Sn满足: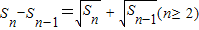 .记数列
.记数列 前n项和为Tn,
前n项和为Tn,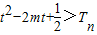 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围. 是函数f(x)=ax的图象上一点,所以a=
是函数f(x)=ax的图象上一点,所以a= ,所以f(x)=
,所以f(x)= ,即可得到数列的前3项,进而求出数列的首项与公比,即可得到数列{an}的通项公式;
,即可得到数列的前3项,进而求出数列的首项与公比,即可得到数列{an}的通项公式; =
= ,所以数列{
,所以数列{ }是以1为首项,以1为公差的等差数列,所以得到Sn,利用bn=Sn-Sn-1求出答案.
}是以1为首项,以1为公差的等差数列,所以得到Sn,利用bn=Sn-Sn-1求出答案. ;进而把原不等式化简为:当m∈[-1,1]时,不等式t2-2mt>0恒成立;设g(m)=-2tm+t2,m∈[-1,1],然后利用函数的有界性解决恒成立问题即可得到答案.
;进而把原不等式化简为:当m∈[-1,1]时,不等式t2-2mt>0恒成立;设g(m)=-2tm+t2,m∈[-1,1],然后利用函数的有界性解决恒成立问题即可得到答案. ,所以f(x)=
,所以f(x)= ,
,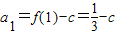 ,a2=[f(2)-c]-[f(1)-c]=
,a2=[f(2)-c]-[f(1)-c]= ,a3=[f(3)-c]-[f(2)-c]=
,a3=[f(3)-c]-[f(2)-c]=
 ,所以c=1.
,所以c=1. ,所以
,所以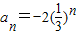 ;
; =
= ,
, ;
; }是以1为首项,以1为公差的等差数列,并且有
}是以1为首项,以1为公差的等差数列,并且有 ;
;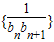 前n项和为Tn,
前n项和为Tn,

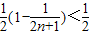 ;
; 恒成立,
恒成立, ,
,

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省泉州一中高二(上)期中数学试卷(文科)(解析版) 题型:解答题
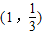 是函数f(x)=ax(a>0,且a≠1)的图象上一点.等比数列{an}的前n项和为f(n)-1.数列{bn}(bn>0)的首项为1,且前n项和sn满足
是函数f(x)=ax(a>0,且a≠1)的图象上一点.等比数列{an}的前n项和为f(n)-1.数列{bn}(bn>0)的首项为1,且前n项和sn满足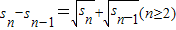
 的前n项和为Tn,问满足Tn>
的前n项和为Tn,问满足Tn> 的最小正整数n是多少?
的最小正整数n是多少?查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省许昌市五校高二(上)第四次联考数学试卷(文科)(解析版) 题型:解答题
 是函数f(x)=ax(a>0,且a≠1)的图象上一点.等比数列{an}的前n项和为f(n)-1.数列{bn}(bn>0)的首项为1,且前n项和sn满足
是函数f(x)=ax(a>0,且a≠1)的图象上一点.等比数列{an}的前n项和为f(n)-1.数列{bn}(bn>0)的首项为1,且前n项和sn满足
 的前n项和为Tn,问满足Tn>
的前n项和为Tn,问满足Tn> 的最小正整数n是多少?
的最小正整数n是多少?查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省泉州一中高二(上)期中数学试卷(文科)(解析版) 题型:解答题
 是函数f(x)=ax(a>0,且a≠1)的图象上一点.等比数列{an}的前n项和为f(n)-1.数列{bn}(bn>0)的首项为1,且前n项和sn满足
是函数f(x)=ax(a>0,且a≠1)的图象上一点.等比数列{an}的前n项和为f(n)-1.数列{bn}(bn>0)的首项为1,且前n项和sn满足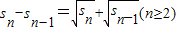
 的前n项和为Tn,问满足Tn>
的前n项和为Tn,问满足Tn>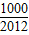 的最小正整数n是多少?
的最小正整数n是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com