
����Ŀ��Ϊ����ƽ̶�ۺ��������ġ��������ε������裬������ij���β��ſ�����һ�����μ����Ʒ��ÿ����Ʒ�ijɱ���12Ԫ�����ۼ���16Ԫ����ƽ������![]() ����������β���ͨ���Ľ����գ��ڱ�֤��Ʒ�ɱ�����Ļ����ϣ���Ʒ�������ͼ�����������ߣ�����������Ʒ���ۼ���ߡ����г������������Ʒ�����ۼ���ߵİٷ���Ϊ
����������β���ͨ���Ľ����գ��ڱ�֤��Ʒ�ɱ�����Ļ����ϣ���Ʒ�������ͼ�����������ߣ�����������Ʒ���ۼ���ߡ����г������������Ʒ�����ۼ���ߵİٷ���Ϊ![]() ����ô��ƽ�����������ٵİٷ���Ϊ
����ô��ƽ�����������ٵİٷ���Ϊ![]() ���ǸĽ����պ����β������۸ü���Ʒ����ƽ��������
���ǸĽ����պ����β������۸ü���Ʒ����ƽ��������![]() ��Ԫ��.
��Ԫ��.
��1���![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2���Ľ����պ�ȷ���ü���Ʒ���ۼۣ�ʹ�����β������۸ü���Ʒ����ƽ���������.
���𰸡���1��![]() ��
��
��2��������Ʒ���ۼ�Ϊ![]() Ԫʱ�������β������۸ü���Ʒ����ƽ���������.
Ԫʱ�������β������۸ü���Ʒ����ƽ���������.
�������������������I��������֪ÿ����Ʒ�����ۼ�Ϊ16��1+x��������ƽ��������Ϊa��1��x2�������������Ƕ��ߵĻ�ȥ���ɱ����������������![]() .
.
��II���ɣ�1����֪�������ʽ����������һԪ���κ�����ϵ�����Զ������ڶ��������о����������ԣ��������ֵ��
��1��������� ![]()
��2���ɣ�1���� ![]()
��![]() ��
�� ![]() �� ��
�� ��![]() ʱ��
ʱ�� ![]() ����
����![]() ʱ��
ʱ�� ![]() ��
��
���� ��![]() ʱ��
ʱ�� ![]() ȡ�����ֵ. ������Ʒ���ۼ�Ϊ
ȡ�����ֵ. ������Ʒ���ۼ�Ϊ![]() Ԫʱ�������β������۸ü���Ʒ����ƽ���������.
Ԫʱ�������β������۸ü���Ʒ����ƽ���������.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����OΪ����ԭ�㣬��P�����꣨x��2��x��y��
��1����һ�������У����б��Ϊ1��2��3�����ſ�Ƭ���ִӴ˺����зŻص��Ⱥ�鵽���ſ�Ƭ�ı�ŷֱ��Ϊx��y����|OP|�����ֵ�������¼���|OP|ȡ�����ֵ���ĸ��ʣ�
��2�������ü���������[0��3]���Ⱥ�ȡ�������ֱ��Ϊx��y����P���ڵ�һ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˵õ�����y=3sin��2x+ ![]() ����ͼ��ֻҪ�Ѻ���y=3sinx��ͼ�������еĵ㣨 ��
����ͼ��ֻҪ�Ѻ���y=3sinx��ͼ�������еĵ㣨 ��
A.���������̵�ԭ���� ![]() ���������겻�䣩���ٰ�����ͼ�����еĵ�����ƽ��
���������겻�䣩���ٰ�����ͼ�����еĵ�����ƽ�� ![]() ����λ����
�������
B.�������쳤��ԭ����2���������겻�䣩���ٰ�����ͼ�����еĵ�����ƽ�� ![]() ����λ����
�������
C.����ƽ�� ![]() ����λ���ȣ��ٰ�����ͼ�����еĵ���������̵�ԭ����
����λ���ȣ��ٰ�����ͼ�����еĵ���������̵�ԭ���� ![]() ���������겻�䣩
���������겻�䣩
D.����ƽ�� ![]() ����λ���ȣ��ٰ�����ͼ�����еĵ�������쳤��ԭ����2���������겻�䣩
����λ���ȣ��ٰ�����ͼ�����еĵ�������쳤��ԭ����2���������겻�䣩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
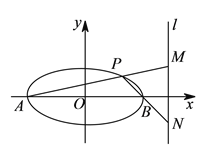
����Ŀ����֪��Բ![]() ��
��![]() �Ǵ���
�Ǵ���![]() �ij����������Ҷ���ֱ�Ϊ
�ij����������Ҷ���ֱ�Ϊ![]() ��
��![]() ����
����![]() ����Բ��λ��
����Բ��λ��![]() ���Ϸ��Ķ��㣬ֱ��
���Ϸ��Ķ��㣬ֱ��![]() ��
��![]() ��ֱ��
��ֱ��![]() �ֱ���
�ֱ���![]() ��
��![]() ���㣨��ֱ��
���㣨��ֱ��![]() ��б��Ϊ������.
��б��Ϊ������.
������ֱ��![]() ��
��![]() ��б�ʷֱ�Ϊ
��б�ʷֱ�Ϊ![]() ��
�� ![]() ����֤
����֤![]() Ϊ��ֵ.
Ϊ��ֵ.
�������߶�![]() �ij��ȵ���Сֵ.
�ij��ȵ���Сֵ.
�����ж���![]() ���������ڵ�
���������ڵ�![]() ��ʹ��
��ʹ��![]() �ǵȱ�����������ʲô��������ֱ��д�������
�ǵȱ�����������ʲô��������ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ���ҽ���Ϊ
���ҽ���Ϊ![]() ��������Ϊ
��������Ϊ![]() ����ֱ��
����ֱ��![]() ��б����
�����![]() ����
����![]() ����Բ
����Բ![]() ����
����![]() ��
�� ![]() ����.
����.
��������Բ�ı�����.
������ֱ��![]() ��
��![]() ���ϵĽؾ���
���ϵĽؾ���![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
������![]() Ϊ�������������Σ�����Ϊ
Ϊ�������������Σ�����Ϊ![]() ����
����![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ���4��23��Ϊ��������գ�Ϊ����ij��Уѧ����ѧ���ࣩܶ�Ķ�������������ȡ��������Ů����20����ɵ�һ�������������ǵ����Ķ�������λ������������ͳ�ƣ������õ����������Ķ�����Ƶ���ֲ�����Ů�����Ķ�����Ƶ�ʷֲ�ֱ��ͼ.
�������Ķ�����Ƶ���ֲ��������Ķ�����������![]() �ڣ�
�ڣ�
![]()
������Ů�����Ķ�����Ƶ�ʷֲ�ֱ��ͼ���Ƹ�УŮ�����Ķ�������λ����
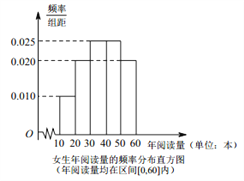
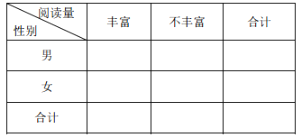
�������겻С��40��Ϊ�Ķ��ḻ������Ϊ�Ķ����ḻ���������������о����Ķ������Ա�Ĺ�ϵ���������![]() �����������ж��Ƿ���99%�İ�����Ϊ�Ķ��ḻ���Ա��йأ�
�����������ж��Ƿ���99%�İ�����Ϊ�Ķ��ḻ���Ա��йأ�
�����������У������Ķ�����![]() ��ѧ���У������ȡ2�˲μ�ȫ�е����ı���������2������������Ϊ
��ѧ���У������ȡ2�˲μ�ȫ�е����ı���������2������������Ϊ![]() ����
����![]() �ķֲ��к�����.
�ķֲ��к�����.
���� 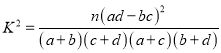 ������
������![]()

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() ��
��![]() .
.
��1��֤��������![]() �ǵȱ����У�
�ǵȱ����У�
��2��������![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��һ�꼶ѧ��ij�������������ܲ��Ե�ԭʼ�ɼ����ðٷ���,��֪������Щѧ����ԭʼ�ɼ����ֲ���![]() ��,�����ɼ�ʹ�õȼ��Ƹ��ȼ����ֱ����±�,�涨��
��,�����ɼ�ʹ�õȼ��Ƹ��ȼ����ֱ����±�,�涨�� ![]() ��
��![]() ��
��![]() ����Ϊ�ϸ�ȼ�,
����Ϊ�ϸ�ȼ�, ![]() Ϊ���ϸ�ȼ�.
Ϊ���ϸ�ȼ�.
�ٷ��� |
|
|
|
|
�ȼ� |
|
|
|
|
Ϊ�˽��У��һ�꼶ѧ�������������,���г�ȡ��![]() ��ѧ����ԭʼ�ɼ���Ϊ��������ͳ��,����
��ѧ����ԭʼ�ɼ���Ϊ��������ͳ��,����![]() �ķ�������Ƶ�ʷֲ�ֱ��ͼ��ͼ
�ķ�������Ƶ�ʷֲ�ֱ��ͼ��ͼ![]() ��ʾ,�����з�����
��ʾ,�����з�����![]() �ּ����ϵ��������ݵľ�Ҷͼ��ͼ
�ּ����ϵ��������ݵľ�Ҷͼ��ͼ![]() ��ʾ.
��ʾ.
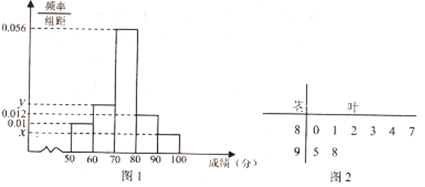
��1����![]() ��Ƶ�ʷֲ�ֱ��ͼ�е�
��Ƶ�ʷֲ�ֱ��ͼ�е�![]() ��ֵ��
��ֵ��
��2�������������������˼�룬���¼�������Ƶ����Ϊ��Ӧ�¼������ĸ��ʣ����ڸ�У��һѧ����ѡ![]() ��,��������
��,��������![]() �˳ɼ��Ǻϸ�ȼ��ĸ��ʣ�
�˳ɼ��Ǻϸ�ȼ��ĸ��ʣ�
��3����ѡȡ��������,��![]() ��
��![]() �����ȼ���ѧ���������ȡ��
�����ȼ���ѧ���������ȡ��![]() ��ѧ�����е���,��
��ѧ�����е���,��![]() ��ʾ����ȡ��
��ʾ����ȡ��![]() ��ѧ����Ϊ
��ѧ����Ϊ![]() �ȼ���ѧ������,���������
�ȼ���ѧ������,���������![]() �ķֲ��м���ѧ����.
�ķֲ��м���ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����{an}�Ĺ��Ϊ�㣬a1=25����a1 �� a11 �� a13�ɵȱ����У�
��1����{an}��ͨ�ʽ��
��2����a1+a4+a7+��+a3n��2 ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com