【答案】
分析:(1)确定函数的定义域,再求导函数,确定函数的单调性,从而可以求函数h(x)的极值;
(2)函数h(x)有两个极值点,等价于导函数为0的方程有两个不相等的正数解,利用韦达定理可解;
(3)利用新定义,先确定“隔离直线”,再进行证明即可.
解答:解:(1)a=1时,f(x)=x
2+x-3,h(x)=x
2+2x-3-4lnx,h(x)的定义域是(0,+∞),
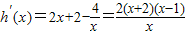
当x∈(0,1)时,h′(x)<0,h(x)递减,
当x∈(1,+∞)时,h′(x)>0,h(x)递增
∴x=1时,h(x)取得极小值h(1)=0,h(x)无极大值.…(4分)
(2)h(x)=ax
2+2x-4lnx-3,x∈(0,+∞),
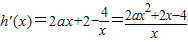
依题意,方程2ax
2+2x-4=0在(0,+∞)上有两个不相等的正数解.
∴
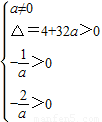
,∴
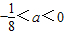
∴a的取值范围是(-

,0)…(9分)
(3)设存在,a=1时,f(x)=x
2+x-3
由(1)知,当且仅当x=1时,h(x)=0,此时,f(1)=g(1)=-1
∴y=f(x)与y=g(x)的图象有唯一的交点A(1,-1)
直线?必过点A,设?的方程:y+1=k(x-1),即y=kx-k-1
由f(x)≥kx-k-1恒成立得x
2+(1-k)x+k-2≥0恒成立
∴△=(1-k)
2-4(k-2)=(k-3)
2≤0
∴k=3,直线?的方程:y=3x-4…(12分)
以下证明g(x)≤3x-4对x>0恒成立
令
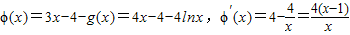
当x∈(0,1)时,ϕ′(x)<0,ϕ(x)递减,当x∈(1,+∞)时,ϕ′(x)>0,ϕ(x)递增,
∴ϕ(x)的最小值为ϕ(1)=0,∴ϕ(x)≥0恒成立
即g(x)≤3x-4对x>0恒成立
综上,f(x)和g(x)存在唯一的“隔离直线”:y=3x-4…(14分)
点评:本题考查导数函数单调性中的应用,考查学生对新定义的理解.解题时要认真审题,注意挖掘题设中的隐含条件,合理地运用导数的性质进行求解.

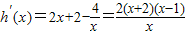
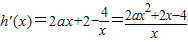
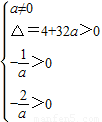 ,∴
,∴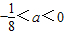
 ,0)…(9分)
,0)…(9分)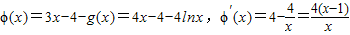


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案