
【题目】 为向国际化大都市目标迈进,沈阳市今年新建三大类重点工程,它们分别是30项基础设施类工程,20项民生类工程和10项产业建设类工程.现有来沈阳的3名工人相互独立地从这60个项目中任选一个项目参与建设.
(Ⅰ)求这3人选择的项目所属类别互异的概率;
(Ⅱ)将此3人中选择的项目属于基础设施类工程或产业建设类工程的人数记为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
科目:高中数学 来源: 题型:
【题目】如图,学校升旗仪式上,主持人站在主席台前沿D处,测得旗杆AB顶部的仰角为![]() 俯角最后一排学生C的俯角为
俯角最后一排学生C的俯角为![]() 最后一排学生C测得旗杆顶部的仰角为
最后一排学生C测得旗杆顶部的仰角为![]() 旗杆底部与学生在一个水平面上,并且不计学生身高.
旗杆底部与学生在一个水平面上,并且不计学生身高.
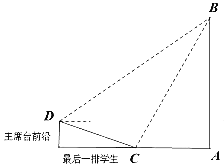
(1)设![]() 米,试用
米,试用![]() 和
和![]() 表示旗杆的高度AB(米);
表示旗杆的高度AB(米);
(2)测得![]() 米,
米,![]() 若国歌长度约为50秒,国旗班升旗手应以多大的速度匀速升旗才能是国旗到达旗杆顶点时师生的目光刚好停留在B处?
若国歌长度约为50秒,国旗班升旗手应以多大的速度匀速升旗才能是国旗到达旗杆顶点时师生的目光刚好停留在B处?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() ,且满足
,且满足![]() .
.
(1)判断函数![]() 在
在![]() 上的单调性,并用定义证明;
上的单调性,并用定义证明;
(2)设函数![]() ,求
,求![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(3)若存在实数m,使得关于x的方程![]() 恰有4个不同的正根,求实数m的取值范围.
恰有4个不同的正根,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学志愿者协会有6名男同学,4名女同学,在这10名同学中,3名同学来自数学学院,其余7名同学来自物理﹑化学等其他互不相同的七个学院,现从这10名同学中随机选取3名同学,到希望小学进行支教活动(每位同学被选到的可能性相同).
(1)求选出的3名同学是来自互不相同学院的概率;
(2)设![]() 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行抽样检查,测得身高情况的统计图如图所示:

(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm的概率;
(3)从样本中身高在180~190cm的男生中任选2人,求至少有1人身高在185~190cm的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为集合
为集合![]() 的子集,且
的子集,且![]() ,若
,若![]() ,则称
,则称![]() 为集合
为集合![]() 的
的![]() 元“大同集”.
元“大同集”.
(1)写出实数集![]() 的一个二元“大同集”;
的一个二元“大同集”;
(2)是否存在正整数集![]() 的二元“大同集”,请说明理由;
的二元“大同集”,请说明理由;
(3)求出正整数集![]() 的所有三元“大同集”.
的所有三元“大同集”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.

![]() 求椭圆E的方程;
求椭圆E的方程;
![]() 若A是椭圆E的左顶点,经过左焦点F的直线l与椭圆E交于C,D两点,求
若A是椭圆E的左顶点,经过左焦点F的直线l与椭圆E交于C,D两点,求![]() 与
与![]() 为坐标原点
为坐标原点![]() 的面积之差绝对值的最大值.
的面积之差绝对值的最大值.
![]() 已知椭圆E上点
已知椭圆E上点![]() 处的切线方程为
处的切线方程为![]() ,T为切点
,T为切点![]() 若P是直线
若P是直线![]() 上任意一点,从P向椭圆E作切线,切点分别为N,M,求证:直线MN恒过定点,并求出该定点的坐标.
上任意一点,从P向椭圆E作切线,切点分别为N,M,求证:直线MN恒过定点,并求出该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com