
【题目】在数列{an}中,若an2﹣an﹣12=p,(n≥2,n∈N*,p为常数),则称{an}为“等方差数列”,下列是对“等方差数列“的判断:
①若{an}是等方差数列,则{an2}是等差数列;
②{(﹣1)n}是等方差数列;
③若{an}是等方差数列,则{akn}(k∈N*,k为常数)也是等方差数列;
④若{an}既是等方差数列,又是等差数列,则该数列为常数列.
其中正确命题的个数是( )
A.1B.2C.3D.4
【答案】D
【解析】
利用等方差数列的定义与等差数列的定义判断①;利用等方差数列的定义判断②;先表示出{akn}的通项公式,然后利用等方差的定义进行判断③;利用等方差数列和等差数列的定义判断④.
①若数列{an}是等方差数列,则有![]() p(n∈N*,且n≥2),
p(n∈N*,且n≥2),
则数列{![]() }是公差为p的等差数列,故①正确;
}是公差为p的等差数列,故①正确;
②数列{(﹣1)n}中,an2﹣an﹣12=[(﹣1)n]2﹣[(﹣1)n﹣1]2=0,(n≥2,n∈N*),
∴数列{(﹣1)n}是等方差数列,故②正确;
③数列{an}中的项列举出来是:a1,a2,…,ak,…,a2k,…
数列{akn}中的项列举出来是:ak,a2k,a3k,…
∵(ak+12﹣ak2)=(ak+22﹣ak+12)=…=a2k2﹣a2k﹣12=p
∴(ak+12﹣ak2)+(ak+22﹣ak+12)+…+(a2k2﹣a2k﹣12)=kp
∴ak(n+1)2﹣akn2=kp,即数列{akn}是等方差数列,故③正确;
④∵数列{an}是等差数列,∴an﹣an﹣1=d1(n≥2).
∵数列{an}是等方差数列,∴an2﹣an﹣12=d2(n≥2),
∴(an+an﹣1)d1=d2,
∴当d1≠0时,![]() 为常数列;
为常数列;
当d1=0,数列{an}为常数列.
则该数列{an}必为常数列,故④正确.
∴正确命题的个数是4个.
故选:D.
本题考查新定义以及等差数列的定义及其应用,考查逻辑思维能力与推理论证能力,是中档题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】给定一个由![]() 个小正方形拼成的棋盘形方格,这些小正方形的颜色黑白相间(如图).
个小正方形拼成的棋盘形方格,这些小正方形的颜色黑白相间(如图).
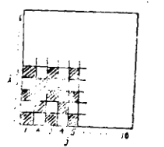
现定义一种运算A:把位于第i行的所有小正方形和位于第j列的所有小正方形都换成相反的颜色,即黑色的小正方形换成白色的,白色的小正方形换成黑色的,这里![]() .我们把A称为在位于第i行第j列上的小正方形上的一次运算.试问:能否经过若干次上述运算把棋盘上的所有小正方形全部换成同一种颜色?证明你的结论.
.我们把A称为在位于第i行第j列上的小正方形上的一次运算.试问:能否经过若干次上述运算把棋盘上的所有小正方形全部换成同一种颜色?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆上,且
在椭圆上,且![]() 轴,
轴,![]() 的周长为6.
的周长为6.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]() 为坐标原点,是否存在常数
为坐标原点,是否存在常数![]() ,使得
,使得![]() 恒成立?请说明理由.
恒成立?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() sin(ωx-
sin(ωx-![]() )(其中ω>0)的图象上相邻两个最高点的距离为π.
)(其中ω>0)的图象上相邻两个最高点的距离为π.
(Ⅰ)求函数f(x)的图象的对称轴;
(Ⅱ)若函数y=f(x)-m在[0,π]内有两个零点x1,x2,求m的取值范围及cos(x1+x2)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,天花板上挂着3串玻璃球,射击玻璃球规则:每次击中1球,每串中下面球没击中,上面球不能击中,则把这6个球全部击中射击方法数是( )
A.78B.60C.48D.36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为某市国庆节7天假期的楼房认购量与成交量的折线图,小明同学根据折线图对这7天的认购量(单位:套)与成交量(单位:套)作出如下判断:①日成交量的中位数是16;②日成交量超过日平均成交量的有2天;③认购量与日期正相关;④10月7日认购量的增幅大于10月7日成交量的增幅.则上述判断正确的个数为( )
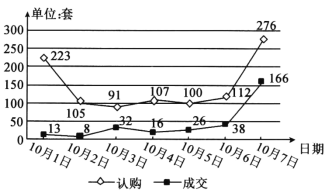
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,焦点到相应准线的距离为
,焦点到相应准线的距离为![]() .
.
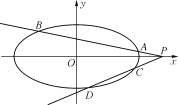
(1) 求椭圆E的标准方程;
(2) 已知P(t,0)为椭圆E外一动点,过点P分别作直线l1和l2,直线l1和l2分别交椭圆E于点A,B和点C,D,且l1和l2的斜率分别为定值k1和k2,求证:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com