
对于具有相同定义域![]() 的函数
的函数![]() 和
和![]() ,若存在函数
,若存在函数![]() (
(![]() 为常数),对任给的正数
为常数),对任给的正数![]() ,存在相应的
,存在相应的![]() ,使得当
,使得当![]() 且
且![]() 时,总有
时,总有![]() 则称直线
则称直线![]()
![]() 为曲线
为曲线![]() 与
与![]() 的“分渐近线”。给出定义域均为D=
的“分渐近线”。给出定义域均为D=![]() 的四组函数如下:
的四组函数如下:
①![]() ,
,![]() ;②
;②![]() ,
,![]()
![]() ;
;
③![]()
![]() ,
,![]()
![]() ;④
;④![]() ,
,![]() 。
。
其中,曲线![]() 与
与![]() 存在“分渐近线”的是
存在“分渐近线”的是
A.①④ B.②③ C.②④ D.③④
科目:高中数学 来源: 题型:
|
| x |
| 2x-3 |
| x |
| x2+1 |
| x |
| xlnx+1 |
| lnx |
| 2x2 |
| x+1 |
| A、①④ | B、②③ | C、②④ | D、③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2x |
| x+2 |
| 2 |
| 3 |
| 5 |
| 8 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
对于具有相同定义域![]() 的函数
的函数![]() 和
和![]() ,若存在函数
,若存在函数![]() (
(![]() 为常数),对任给的正数
为常数),对任给的正数![]() ,存在相应的
,存在相应的![]() ,使得当
,使得当![]() 且
且![]() 时,总有
时,总有![]() 则称直线
则称直线![]()
![]() 为曲线
为曲线![]() 与
与![]() 的“分渐近线”。给出定义域均为D=
的“分渐近线”。给出定义域均为D=![]() 的四组函数如下:
的四组函数如下:
①![]() ,
,![]() ;②
;②![]() ,
,![]()
![]() ;
;
③![]()
![]() ,
,![]()
![]() ;④
;④![]() ,
,![]() 。
。
其中,曲线![]() 与
与![]() 存在“分渐近线”的是
存在“分渐近线”的是
A.①④ B.②③ C.②④ D.③④
查看答案和解析>>
科目:高中数学 来源:2014届湖北省教学合作高三10月联考文科数学试卷(解析版) 题型:填空题
对于具有相同定义域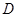 的函数
的函数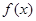 和
和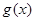 ,若存在
,若存在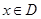 ,使得
,使得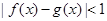 ,则
,则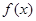 和
和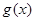 在
在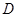 上是“亲密函数”.给出定义域均为
上是“亲密函数”.给出定义域均为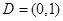 的四组函数如下:
的四组函数如下:
① ②
②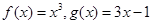
③ 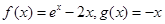 ④
④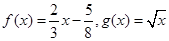
其中,函数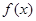 和
和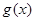 在
在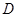 上是“亲密函数”的是
.
上是“亲密函数”的是
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com