
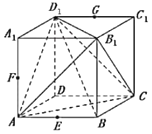
【题目】已知正方体ABCD-A1B1C1D1的棱长为a,点E,F,G分别为棱AB,AA1,C1D1的中点.下列结论中,正确结论的序号是______.
①过E,F,G三点作正方体的截面,所得截面为正六边形;
②B1D1∥平面EFG;
③BD1⊥平面ACB1;
④异面直线EF与BD1所成角的正切值为![]() ;
;
⑤四面体ACB1D1的体积等于![]() a3
a3
【答案】①③④
【解析】
根据公理3,作截面可知①正确;根据直线与平面的位置关系可知②不正确;根据线面垂直的判定定理可知③正确;根据异面直线所成的角的定义求得异面直线EF与BD1的夹角的正切值为![]() ,可知④正确;用正方体体积减去四个正三棱锥的体积可知⑤不正确.
,可知④正确;用正方体体积减去四个正三棱锥的体积可知⑤不正确.
解:延长EF分别与B1A1,B1B的延长线交于N,Q,连接GN交A1D1于H,
设HG与B1C1的延长线交于P,连接PQ交CC1于I,交BC于M,
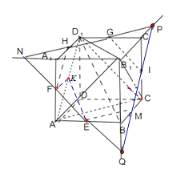
连FH,HG,GI,IM,ME,则截面六边形EFHGIM为正六边形,故①正确;
B1D1与HG相交,故B1D1与平面 EFG相交,所以②不正确;
∵BD1⊥AC,BD1⊥B1C,且AC与B1C相交,所以BD1⊥平面ACB1,故③正确;
取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
所以![]() 就是异面直线EF与BD1的夹角,
就是异面直线EF与BD1的夹角,
设正方体的边长为![]() ,可得:
,可得:![]() ,
,![]() ,
,![]() ,
,
所以![]() 是直接三角形.可得:
是直接三角形.可得:![]() .
.
可得异面直线EF与BD1的夹角的正切值为![]() ,故④正确;
,故④正确;
四面体ACB1D1的体积等于正方体的体积减去四个正三棱锥的体积,
即为![]() ,故⑤不正确.
,故⑤不正确.
故答案为:①③④


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】“一带一路”近年来成为了百姓耳熟能详的热门词汇,对于旅游业来说,“一带一路”战略的提出,让“丝路之旅”超越了旅游产品、旅游线路的简单范畴,赋予了旅游促进跨区域融合的新理念. 而其带来的设施互通、经济合作、人员往来、文化交融更是将为相关区域旅游发展带来巨大的发展机遇.为此,旅游企业们积极拓展相关线路;各地旅游主管部门也在大力打造丝路特色旅游品牌和服务.某市旅游局为了解游客的情况,以便制定相应的策略. 在某月中随机抽取甲、乙两个景点10天的游客数,统计得到茎叶图如下:

(1)若将图中景点甲中的数据作为该景点较长一段时期内的样本数据,以每天游客人数频率作为概率.今从这段时期内任取4天,记其中游客数超过130人的天数为![]() ,求概率
,求概率![]() ;
;
(2)现从上图20天的数据中任取2天的数据(甲、乙两景点中各取1天),记其中游客数不低于125且不高于135人的天数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱柱![]() 中,底面
中,底面![]() 为正方形,
为正方形, ![]() 平面
平面![]() 为棱
为棱![]() 的中点,
的中点, ![]() 为棱
为棱![]() 的中点,
的中点, ![]() 为棱
为棱![]() 的中点.
的中点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,棱
,棱![]() 上有一点
上有一点![]() ,且
,且![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某片经济林的生长情况,随机测量其中的100棵树的底部周长,得到如下数据(单位:cm):
135 98 102 110 99 121 110 96 100 103
125 97 117 113 110 92 102 109 104 112
109 124 87 131 97 102 123 104 104 128
105 123 111 103 105 92 114 108 104 102
129 126 97 100 115 111 106 117 104 109
111 89 110 121 80 120 121 104 108 118
129 99 90 99 121 123 107 111 91 100
99 101 116 97 102 108 101 95 107 101
102 108 117 99 118 106 119 97 126 108
123 119 98 121 101 113 102 103 104 108
(1)列出频率分布表;
(2)画出频率分布直方图与频率折线图;
(3)估计该片经济林中底部周长小于100cm的树占多少,底部周长不小于120cm的树占多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z=![]() ,(m∈R,i是虚数单位).
,(m∈R,i是虚数单位).
(1)若z是纯虚数,求m的值;
(2)设![]() 是z的共轭复数,复数
是z的共轭复数,复数![]() +2z在复平面上对应的点在第一象限,求m的取值范围.
+2z在复平面上对应的点在第一象限,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理是合情推理的是( )
①由圆的性质类比出球的有关性质;②由直角三角形、等腰三角形、等边三角形内角和是![]() 归纳出所有三角形的内角和都是
归纳出所有三角形的内角和都是![]() ;③由
;③由![]() ,满足
,满足![]() ,
,![]() ,推出
,推出![]() 是奇函数;④三角形内角和是
是奇函数;④三角形内角和是![]() ,四边形内角和是
,四边形内角和是![]() ,五边形内角和是
,五边形内角和是![]() ,由此得凸多边形内角和是
,由此得凸多边形内角和是![]() .
.
A. ①②B. ①③④C. ①②④D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的方程为
的方程为![]() ,
,![]() 点的坐标为
点的坐标为![]() .
.
(1)求过点![]() 且与圆
且与圆![]() 相切的直线方程;
相切的直线方程;
(2)过点![]() 任作一条直线
任作一条直线![]() 与圆
与圆![]() 交于不同两点
交于不同两点![]() ,
,![]() ,且圆
,且圆![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() ,求证:直线
,求证:直线![]() 与
与![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f (x)在R上可导,其导函数为f ′(x),且函数f (x)在x=-2处取得极大值,则函数y=![]() f ′(x)的图象可能是
f ′(x)的图象可能是
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com