【题目】已知圆
：
，直线
：
，圆上的点
到直线的距离小于2的概率为（ ）
A. 
B. 
C. 
D. 
智能训练练测考系列答案
计算高手系列答案科目：高中数学 来源： 题型：
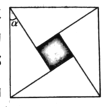
【题目】中国古代的数学家们最早发现并应用勾股定理，而最先对勾股定理进行证明的是三国时期的数学家赵爽.赵爽创制了一幅“勾股圆方图”，用数形结合的方法，给出了勾股定理的详细证明。在这幅“勾股圆方图”中，
个相等的直角三角形再加上中间的那个小正方形组成一个大的正方形。若直角三角形的较小锐角
的正切值为
，现向该正方形区域内投掷-枚飞镖，则飞镖落在小正方形内(阴影部分)的概率是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】容器中盛有5个白乒乓球和3个黄乒乓球．
(1)“从8个球中任意取出1个，取出的是白球”与“从剩下的7个球中任意取出1个，取出的还是白球”这两个事件是否相互独立？为什么？
(2)“从8个球中任意取出1个，取出的是白球”与“把取出的1个白球放回容器，再从容器中任意取出1个，取出的是黄球”这两个事件是否相互独立？为什么？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，角A，B，C的对边分别为a，b，c，且（c﹣2a） 
=c 
（1）求B的大小；
（2）已知f（x）=cosx（asinx﹣2cosx）+1，若对任意的x∈R，都有f（x）≤f（B），求函数f（x）的单调递减区间．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在正方体ABCD－A1B1C1D1中，下列说法正确的是____ (填序号).
(1)直线AC1在平面CC1B1B内．
(2)设正方形ABCD与A1B1C1D1的中心分别为O、O1，则平面AA1C1C与平面BB1D1D的交线为OO1.
(3)由A、C1、B1确定的平面是ADC1B1.
(4)由A、C1、B1确定的平面与由A、C1、D确定的平面是同一个平面．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系xOy中，以O为极点，x轴正半轴为极轴建立极坐标系，圆C的极坐标方程为ρ＝2
cos
，直线l的参数方程为
(t为参数)，直线l与圆C交于A，B两点，P是圆C上不同于A，B的任意一点．
(1)求圆心的极坐标；
(2)求△PAB面积的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】根据下列对几何体结构特征的描述，说出几何体的名称．
（1）由八个面围成，其中两个面是互相平行且全等的正六边形，其它各面都是矩形；
（2）一个等腰梯形绕着两底边中点的连线所在的直线旋转180°形成的封闭曲面所围成的几何体；
（3）由五个面围成，其中一个面是正方形，其他各面都是有一个公共顶点的全等三角形；
（4）一个圆绕其一条直径所在的直线旋转180°形成的封闭曲面所围成的几何体．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
