
分析 根据函数零点与对应方程根之间的关系,我们可将f(x)存在零点转化为方程log2(a-2x)=1-x有根,结合对数方程和指数方程的解法,我们可将他转化为一个二次方程根的存在性总是,再根据二次方程根的个数与△的关系及韦达定理,我们易构造一个关于a的不等式,解不等式即可求出实数a的取值范围.
解答 解:若f(x)存在零点,
则方程log2(a-2x)=1-x有根
即21-x=a-2x有根,
令2x=t(t>0)
则原方程等价于$\frac{2}{t}$=a-t有正根
即t2-at+2=0有正根,
根据根与系数的关系t1t2=2>0,
即若方程有正根,必有两正根,
故有$\left\{\begin{array}{l}{{t}_{1}+{t}_{2}=a>0}\\{{a}^{2}-8≥0}\end{array}\right.$,∴a≥2$\sqrt{2}$.
故答案为:$a≥2\sqrt{2}$.
点评 本题考查的知识点是函数零点的判定定理,其中根据指数方程和对数方程的解法,将函数对应的方程转化为一个二次方程是解答的关键.


科目:高中数学 来源: 题型:解答题
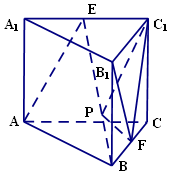 在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.
在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ac>bc | B. | $\frac{b}{a}$>1 | C. | |a|>|b| | D. | ($\frac{1}{2}$)a<($\frac{1}{2}$)b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 环数 | 10 | 9 | 8 | 7 | 7以下 |
| 概率 | 0.25 | 0.3 | 0.2 | 0.15 | N |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com