
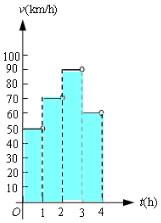
 一辆汽车在某段路程中的行驶速率与时间的关系如图所示.
一辆汽车在某段路程中的行驶速率与时间的关系如图所示.分析 (1)由频率分布图能求出阴影部分的面积,表示汽车在4小时内行驶的路程.
(2)由这辆汽车在行驶该段路程前里程表的读数是8018km,结合频率分布直方图能求出汽车在行驶这段路程时里程表读数s(km)与时间t (h)的函数解析式,并能作出图象.
解答 解:(1)阴影部分的面积为:
50+70+90+60=270,
表示汽车在4小时内行驶的路程为270 km. (4分)
(2)∵这辆汽车在行驶该段路程前里程表的读数是8018km,
汽车在行驶这段路程时里程表读数s(km)与时间t (h)的函数解析式为:
$s=\left\{\begin{array}{l}50t+8018,0≤t<1\\ 70(t-1)+8068,1≤t<2\\ 90(t-2)+8138,2≤t<3\\ 60(t-3)+8228,3≤t≤4.\end{array}\right.$(4分)
图象如下图: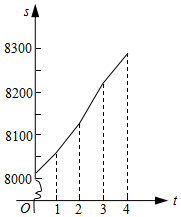
(4分)
点评 本题考查阴影面积的求法,考查函数解析式及图象的求法,是基础题,解题时要认真审题,注意频率分布直方图的性质的合理运用.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$或$\frac{11}{32}$ | B. | $\frac{1}{2}$或$\frac{31}{32}$ | C. | $\frac{11}{32}$或$\frac{31}{32}$ | D. | $\frac{11}{32}$或$\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(|x|)=x+1 | B. | f(x2)=2x+1 | C. | f(|x|)=x2+2 | D. | f($\sqrt{x}$)=3x+2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com