
【题目】如图所示,四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]()
![]() ,
,![]() 为
为![]() 的中点.
的中点.
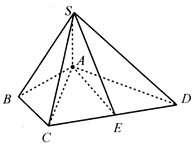
(1)求证:![]() ;
;
(2)求点D与平面![]() 的距离.
的距离.
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)在![]() 中,由余弦定理可解得
中,由余弦定理可解得![]() ,可知
,可知![]() 是直角三角形,又
是直角三角形,又![]() 为等边三角形,所以
为等边三角形,所以![]() ,所以
,所以![]() ,即可证明
,即可证明![]() 平面
平面![]() (2)由(1)可知
(2)由(1)可知![]() ,以点
,以点![]() 为原点,以
为原点,以![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,利用空间向量可求直线
轴建立空间直角坐标系,利用空间向量可求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由余弦定理可得:![]()
解得:![]()
所以![]() ,所以
,所以![]() 是直角三角形,
是直角三角形,
又![]() 为
为![]() 的中点,所以
的中点,所以![]() ,又
,又![]() ,所以
,所以![]() 为等边三角形,
为等边三角形,
所以![]() ,所以
,所以![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)由(1)可知![]() ,以点
,以点![]() 为原点,以
为原点,以![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() .
.
设![]() 为平面
为平面![]() 的法向量,则
的法向量,则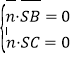 ,即
,即![]()
设![]() ,则
,则![]() ,
,![]() ,即平面
,即平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以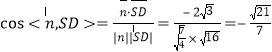
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】下列命题中正确的个数是( )
①由五个面围成的多面体只能是三棱柱;
②由若干个平面多边形所围成的几何体是多面体;
③仅有一组对面平行的五面体是棱台;
④有一面是多边形,其余各面是三角形的几何体是棱锥.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=4,E为DC边的中点,沿AE将△ADE折起,在折起过程中,有几个正确( )

①ED⊥平面ACD ②CD⊥平面BED
③BD⊥平面ACD ④AD⊥平面BED
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】西光厂眼镜车间接到一批任务,需要加工6000个![]() 型零件和2000个
型零件和2000个![]() 型零件.这个车间有214名工人,他们每一个人加工5个
型零件.这个车间有214名工人,他们每一个人加工5个![]() 型零件的时间可以加工3个
型零件的时间可以加工3个![]() 型零件.将这些工人分成两组,两组同时工作,每组加工一种型号的零件,为了在最短的时间内完成这批任务,应怎样分组?
型零件.将这些工人分成两组,两组同时工作,每组加工一种型号的零件,为了在最短的时间内完成这批任务,应怎样分组?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面边长为![]() 、高为
、高为![]() 的正六棱柱
的正六棱柱![]() 展厅内,长为
展厅内,长为![]() ,宽为
,宽为![]() 的矩形油画
的矩形油画![]() 挂在厅内正前方中间.
挂在厅内正前方中间.
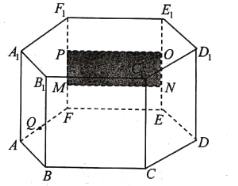
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当游客![]() 在
在![]() 上看油画的纵向视角(即
上看油画的纵向视角(即![]() )最大时,求
)最大时,求![]() 与油画平面所成的角.
与油画平面所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为抗击疫情,中国人民心连心,向世界展示了中华名族的团结和伟大,特别是医护工作者被人们尊敬的称为“最美逆行者”,各地医务工作者主动支援湖北武汉.现有7名医学专家被随机分配到“雷神山”、“火神山”两家医院.
(1)求7名医学专家中恰有两人被分配到“雷神山”医院的概率;
(2)若要求每家医院至少一人,设![]() ,
,![]() 分别表示分配到“雷神山”、“火神山”两家医院的人数,记
分别表示分配到“雷神山”、“火神山”两家医院的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com