
(本小题8分)已知三棱锥A—BCD及其三视图如图所示.

(1)求三棱锥A—BCD的体积与点D到平面ABC的距离;
(2)求二面角 B-AC-D的正弦值.
(1)  ;(2)二面角 B-AC-D的正弦值是
;(2)二面角 B-AC-D的正弦值是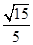 。
。
【解析】考查线面平行、线线垂直的判定定理以及体积的求解.涉及到的知识点比较多,知识性技巧性都很强,属于中档题
(1)利用三视图可知△ABC为直角三角形,∠DBC为直角,AD⊥面DBC,DB=BC=1,AD=2,则DE的长为点D到面ABC的距离,以及三棱锥的体积可得。
(2)作DF⊥AC于点F,连结EF,
∵DE⊥面ABC ∴DE⊥AC ∴AC⊥面DEF ∴AC⊥EF
∴∠DFE是二面角 B-AC-D的平面角从而解三角形可知。
(1)

由三视图可得△ABC为直角三角形,∠DBC为直角,AD⊥面DBC,DB=BC=1,AD=2…………….2分
作DE⊥AB于点E
∵AD⊥面DBC,∴AD⊥BC
∵∠DBC为直角 ∴BC⊥面ADB
∴BC⊥DE
∴DE⊥面ABC………3分
∴DE的长为点D到面ABC的距离
∵DB=1,AD=2 ∴DE=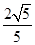 ∴点D到平面ABC的距离为
∴点D到平面ABC的距离为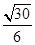 ………4分
………4分
∵ ,∴
,∴ ………5分
………5分
(2) 作DF⊥AC于点F,连结EF,
∵DE⊥面ABC ∴DE⊥AC ∴AC⊥面DEF ∴AC⊥EF
∴∠DFE是二面角 B-AC-D的平面角………7分
∵DB=BC=1 ∴DC= ∴DF=
∴DF=
∴sin∠DFE= 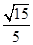
∴二面角 B-AC-D的正弦值是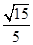 ………8分
………8分


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源:2010-2011年甘肃省兰州一中高二第二学期期中考试数学 题型:解答题
(理)(本题8分)甲、乙、丙三人进行某项比赛,每局有两人参加,没有平局,在一局比赛中,甲胜乙的概率为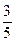 ,甲胜丙的概率为
,甲胜丙的概率为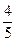 ,乙胜丙的概率为
,乙胜丙的概率为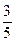 ,比赛的规则是先由甲和乙进行第一局的比赛,然后每局的获胜者与未参加此局比赛的人进行下一局的比赛,在比赛中,有人获胜两局就算取得比赛的胜利,比赛结束.
,比赛的规则是先由甲和乙进行第一局的比赛,然后每局的获胜者与未参加此局比赛的人进行下一局的比赛,在比赛中,有人获胜两局就算取得比赛的胜利,比赛结束.
(1)求只进行两局比赛,甲就取得 胜利的概率;
胜利的概率;
(2)求只进行两局比赛,比赛就结束的概率;
(3)求甲取得比赛胜利的概率.
20、(文)(本小题8分)甲、乙两人做定点投篮,投篮者若投中则继续投篮,否则由对方投篮,第一次甲投篮,已知甲、乙每次投篮命中的概率分别为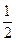 、
、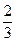 ,且甲、乙投篮是否命中互不影响.
,且甲、乙投篮是否命中互不影响.
(1)求第三次由乙投篮的概率;
(2)求前4次投篮中各投两次的概率.
查看答案和解析>>
科目:高中数学 来源:2010-2011年甘肃省高二第二学期期中考试数学 题型:解答题
(理)(本题8分)甲、乙、丙三人进行某项比赛,每局有两人参加,没有平局,在一局比赛中,甲胜乙的概率为 ,甲胜丙的概率为
,甲胜丙的概率为 ,乙胜丙的概率为
,乙胜丙的概率为 ,比赛的规则是先由甲和乙进行第一局的比赛,然后每局的获胜者与未参加此局比赛的人进行下一局的比赛,在比赛中,有人获胜两局就算取得比赛的胜利,比赛结束.
,比赛的规则是先由甲和乙进行第一局的比赛,然后每局的获胜者与未参加此局比赛的人进行下一局的比赛,在比赛中,有人获胜两局就算取得比赛的胜利,比赛结束.
(1)求只进行两局比赛,甲就取得胜利的概率;
(2)求只进行两局比赛,比赛就结束的概率;
(3)求甲取得比赛胜利的概率.
20、(文)(本小题8分)甲、乙两人做定点投篮,投篮者若投中则继续投篮,否则由对方投篮,第一次甲投篮,已知甲、乙每次投篮命中的概率分别为 、
、 ,且甲、乙投篮是否命中互不影响.
,且甲、乙投篮是否命中互不影响.
(1)求第三次由乙投篮的概率;
(2)求前4次投篮中各投两次的概率.
查看答案和解析>>
科目:高中数学 来源:浙江省富阳市2009-2010学年度高一数学期中试卷 题型:解答题
(本小题满分8分)已知 、
、 、
、 为
为 的三内角,且其对边分别为
的三内角,且其对边分别为 、
、 、
、 ,若
,若 .
.
(1)求 ; (2)若
; (2)若 ,求
,求 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com